
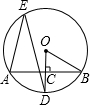
 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB=10$\sqrt{3}$.
如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB=10$\sqrt{3}$. 分析 由垂径定理可证AC=BC,$\widehat{AD}$=$\widehat{BD}$,由30°的圆周角可求得圆心角∠BOD=60°,在RT△OBC中,解正弦函数求得BC,进而求得AB的长度.
解答 解:∵OD⊥AB,
∴AC=BC,$\widehat{AD}$=$\widehat{BD}$,
∵∠AED=30°,
∴∠BOD=2∠AED=60°,
在RT△OBC中,sin∠COB=$\frac{BC}{OB}$,
∴OB=10,
∴$\frac{\sqrt{3}}{2}$=$\frac{BC}{10}$,
∴AB=2BC=10$\sqrt{3}$.
故答案为10$\sqrt{3}$.
点评 本题考查了:①圆周角与圆心角:同弧或等弧所对的圆周角等于圆心角的一半;②垂径定理:垂直于弦的直径平分线并且平分弦所在的弧,③解直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
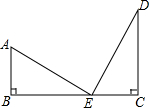 如图,有两根直杆AB,CD隔河相对,AB高20m,CD高30m,两杆相距50m,现两杆杆顶上各有一只鱼鹰,它们同时看到两杆之间河面上E处浮起的一条小鱼,于是以同样的速度同时飞下来争夺该鱼,结果两只鱼鹰同时到达,叼住小鱼,两杆杆底到E处的水平距离各是多少米?
如图,有两根直杆AB,CD隔河相对,AB高20m,CD高30m,两杆相距50m,现两杆杆顶上各有一只鱼鹰,它们同时看到两杆之间河面上E处浮起的一条小鱼,于是以同样的速度同时飞下来争夺该鱼,结果两只鱼鹰同时到达,叼住小鱼,两杆杆底到E处的水平距离各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com