
 如图,我市某中学课外活动小组的同学要测量海河某段流域的宽度,小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处188米远的B处测得∠CBD=30°,根据这些数据计算出这段流域的河宽和BC的长.
如图,我市某中学课外活动小组的同学要测量海河某段流域的宽度,小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处188米远的B处测得∠CBD=30°,根据这些数据计算出这段流域的河宽和BC的长.分析 先构造出直角三角形,设CE=x,根据锐角三角函数表示出AE,BE,BC,用AB=BE-AE建立方程求解即可.
解答 解:如图,过点C作CE⊥AB,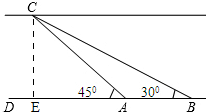 e
e
设CE=x,
在Rt△ACE中,∠CAE=45°,
∴AE=CE=x,
在Rt△BCE中,∵∠CAE=30°,
∴BE=$\sqrt{3}$CE=$\sqrt{3}$x,BC=2x,
∵AB=188,
∴BE-AE=$\sqrt{3}$x-x=188,
∴x=$\frac{188}{\sqrt{3}-1}$≈257m,
∴CE=257m,BC=2x=514m,
即:这段流域的河宽为257m,BC的长为514m;
点评 此题是解直角三角形的应用,主要考查锐角三角函数,勾股定理,解本题的关键是构造出直角三角形,也是解本题的难点,此题需要用方程的思想解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 17cm | B. | 3cm | C. | 17cm或3cm | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3m2-6mn+3n2=3(m-n)2 | B. | x2b+ab2+ab=ab(a+b+1) | ||
| C. | mx2-4m=m(x-2)(x+2) | D. | x2+12x+36=(x+6)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com