
| 小区A | 小区B | |||
| 路程(千米) | 运算单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | D | 0.25 | 32 | 0.25 |
| 乙地 | 22 | 0.3 | 30 | 0.3 |
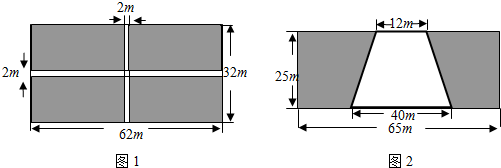
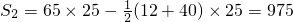 .
. 所以600≤x≤1575.
所以600≤x≤1575. ,由此可以求出 自变量x的取值范围,又由题意可以得到y=30×0.25x+22×0.3(1800-x)+32×0.25(1575-x)+30×0.3(x-600)
,由此可以求出 自变量x的取值范围,又由题意可以得到y=30×0.25x+22×0.3(1800-x)+32×0.25(1575-x)+30×0.3(x-600)

科目:初中数学 来源: 题型:
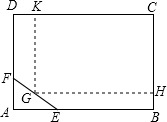 为了使文物保护区△AEF不被破坏,矩形公园的顶点G不能在文物保护区内,已知AB=200m,AD=160m,AE=60m;AF=40m.
为了使文物保护区△AEF不被破坏,矩形公园的顶点G不能在文物保护区内,已知AB=200m,AD=160m,AE=60m;AF=40m.查看答案和解析>>
科目:初中数学 来源: 题型:
| 小区A | 小区B | |||
| 路程(千米) | 运算单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | D | 0.25 | 32 | 0.25 |
| 乙地 | 22 | 0.3 | 30 | 0.3 |
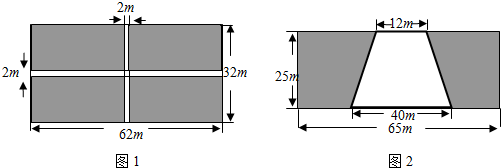
查看答案和解析>>
科目:初中数学 来源: 题型:
|
| 时间t(月) | … | 4 | 5 | 6 | 7 | … | ||||||
| 每件进价Q(元) | … |
|
|
4 |
|
… |
查看答案和解析>>
科目:初中数学 来源:2010年重庆市渝中区中考数学模拟试卷(解析版) 题型:解答题
| 小区A | 小区B | |||
| 路程(千米) | 运算单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | D | 0.25 | 32 | 0.25 |
| 乙地 | 22 | 0.3 | 30 | 0.3 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com