
如下图,⊙O的直径AB为10 cm,弦AC为6 cm,∠ACB的平分线交AB于E,交⊙O于D.求弦AD、CD的长.
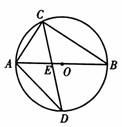
解:∵ AB是直径,∴ ∠ACB = 90°.
在Rt△ABC中,BC =![]() = 8(cm).
= 8(cm).
∵ CD平分∠ACB, ∴ ![]() =
=![]() ,进而AD = BD.
,进而AD = BD.
于是在Rt△ABD中,得 AD = BD =![]() AB = 5
AB = 5![]() (cm).
(cm).
过E作EF⊥AC于F,EG⊥BC于G,F、G是垂足,则四边形CFEG是正方形.
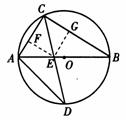
设EF = EG = x,由三角形面积公式,得 ![]() AC ? x +
AC ? x +![]() BC ? x =
BC ? x =![]() AC ? BC,
AC ? BC,
即 ![]() ×6 ? x + 12×8×x = 12×6×8,解得 x =
×6 ? x + 12×8×x = 12×6×8,解得 x =![]() .
.
∴ CE = 2x =![]() .
.
由 △ADE∽△CBE,得 DE : BE = AE : CE = AD : BC,
即 DE : BE = AE :![]() = 5
= 5![]() : 8,
: 8,
解得 AE =![]() ,BE = AB-AE = 10-
,BE = AB-AE = 10-![]() =
=![]() , ∴ DE =
, ∴ DE =![]() .
.
因此 CD = CE + DE =![]() +
+![]() = 7
= 7![]() (cm).
(cm).
答:AD、CD的长依次为5![]() cm,7
cm,7![]() cm.
cm.
说明:另法一 求CD时还可以作CG⊥AE,垂足为G,连接OD.

另法二 过A作AF⊥CD于F,则△ACF是等腰直角三角形.


科目:初中数学 来源:2009年浙江省宁波市中考数学试卷 题型:044
已知:如下图,⊙O的直径AB与弦CD相交于E,弧BC=弧BD,⊙O的切线BF与弦AD的延长线相交于点F.
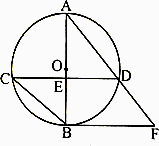
(1)求证:CD∥BF.
(2)连结BC,若⊙O的半径为4,cos∠BCD=![]() ,求线段AD、CD的长.
,求线段AD、CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如下图,⊙O 的直径AB=12cm。AM、BN是两条切线,DC切⊙O 于E,交AM于D,交BN于C,设AD=![]() ,BC=
,BC=![]() 。
。
(1)求![]() 与
与![]() 的函数关系式,并说明是什么函数?
的函数关系式,并说明是什么函数?
(2)若![]() ,求△COD的面积;
,求△COD的面积;
(3)在(2)的条件下,以B为坐标原点,BC为![]() 轴的正半轴,BA为
轴的正半轴,BA为![]() 轴的正半轴, 建立坐标系,求直线CD的解析式。
轴的正半轴, 建立坐标系,求直线CD的解析式。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市九年级第一学期期中考试数学试卷(解析版) 题型:选择题
如下图:⊙O的直径为10,弦AB的长为8,点P是弦AB上的一个动点,使线段OP的长度为整数的点P有( )
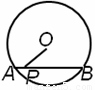
A.3 个 B.4个 C.5个 D.6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com