
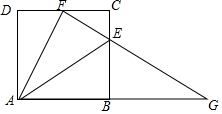
 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.分析 (1)先根据正方形边长得CF=2,由平行相似得:△FCE∽△GBE,则$\frac{FC}{BG}=\frac{CE}{BE}$,代入求得BG=6,根据勾股定理得:EG=3$\sqrt{5}$;
(2)根据已知边的长度分别求$\frac{EC}{FD}$=$\frac{1}{2}$,$\frac{CF}{AD}$=$\frac{2}{4}$=$\frac{1}{2}$,则$\frac{EC}{FD}=\frac{CF}{AD}$,再由正方形性质得:∠C=∠D=90°,则△ECF∽△FDA;
(3)先根据(2)中的△ECF∽△FDA,得∠CFE=∠DAF,$\frac{EF}{FA}=\frac{CE}{DF}=\frac{1}{2}$,证明∠EFA=90°,分别计算∠EAB与∠EAF的正切值,根据两锐角正切大的角大,得出结论.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=CD=BC=4,∠ABC=90°,DC∥AB,
∵CF=DF,
∴CF=$\frac{1}{2}$CD=2,
∵DC∥AG,
∴△FCE∽△GBE,
∴$\frac{FC}{BG}=\frac{CE}{BE}$,
∵$\frac{CE}{BE}$=$\frac{1}{3}$,
∴$\frac{FC}{BG}$=$\frac{1}{3}$,BE=$\frac{3}{4}$BC=$\frac{3}{4}$×4=3,
∴$\frac{2}{BG}=\frac{1}{3}$,
∴BG=6,
在Rt△BEG中,EG=$\sqrt{B{E}^{2}+B{G}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$;
故答案为:3$\sqrt{5}$;
(2)∵四边形ABCD是正方形,
∴BC=AD=DC=4,∠C=∠D=90°,
∵DF=FC=2,CE=1,
∴$\frac{EC}{FD}$=$\frac{1}{2}$,$\frac{CF}{AD}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴$\frac{EC}{FD}=\frac{CF}{AD}$,
∴△ECF∽△FDA;
(3)∵△ECF∽△FDA,
∴∠CFE=∠DAF,$\frac{EF}{FA}=\frac{CE}{DF}=\frac{1}{2}$,
∵∠DFA+∠DAF=90°,
∴∠CFE+∠DFA=90°,
∴∠EFA=90°,
∴tan∠EAF=$\frac{EF}{FA}$=$\frac{1}{2}$,
∵$\frac{CE}{BC}=\frac{1}{4}$,
∴tan∠EAB=$\frac{EB}{AB}=\frac{3}{4}$,
∴$\frac{1}{2}<\frac{3}{4}$,
∴∠EAF<∠EAB.
点评 本题是相似形的综合题,考查了相似三角形的性质和判定,把勾股定理与三角函数相结合,求正方形相关的边的长度,同时利用相似的对应角相等证明∠EFA=90°,得直角三角形,利用锐角的正切值,两锐角正切大的角大,判断角的大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-4,x=2 | B. | m=4,x=2 | C. | m=-4,x=-2 | D. | m=4,x=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1的平方根是-1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{2}$是2的平方根 | D. | ±3是$\sqrt{(-3)^{2}}$的平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题:如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用直尺和圆规画出灯柱的位置点P.(保留作图痕迹)
作图题:如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用直尺和圆规画出灯柱的位置点P.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com