
分析 设小丽第一次购书的原价为x元,则第二次购书的原价为3x元,分x≤$\frac{100}{3}$、$\frac{100}{3}$<x≤$\frac{200}{3}$、$\frac{200}{3}$<x≤100及x>100四种情况,找出关于x的一元一次方程,解之即可得出结论.
解答 解:设小丽第一次购书的原价为x元,则第二次购书的原价为3x元,
根据题意得:当3x≤100,即x≤$\frac{100}{3}$时,x+3x=229.4,
解得:x=57.35(舍去);
当100<3x≤200,即$\frac{100}{3}$<x≤$\frac{200}{3}$时,x+0.9×3x=229.4,
解得:x=62,
∴x+3x=248;
当3x>200且x≤100,即$\frac{200}{3}$<x≤100时,x+0.7×3x=229.4,
解得:x=74,
∴x+3x=296;
当x>100时,0.9x+0.7×3x=229.4,
解得:x≈76.47(舍去).
答:小丽这两次购书原价的总和是248元或296元.
点评 本题考查了一元一次方程的应用,分x≤$\frac{100}{3}$、$\frac{100}{3}$<x≤$\frac{200}{3}$、$\frac{200}{3}$<x≤100及x>100四种情况,列出关于x的一元一次方程是解题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
 阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.| 组别 | 时间(小时) | 频数(人数) | 频率 |
| A | 0≤t≤0.5 | 6 | 0.15 |
| B | 0.5≤t≤1 | a | 0.3 |
| C | 1≤t≤1.5 | 10 | 0.25 |
| D | 1.5≤t≤2 | 8 | b |
| E | 2≤t≤2.5 | 4 | 0.1 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~49人 | 50~100人 | 100人以上 |
| 每人门票价 | 130元 | 110元 | 90元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
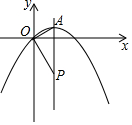 已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).
已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com