
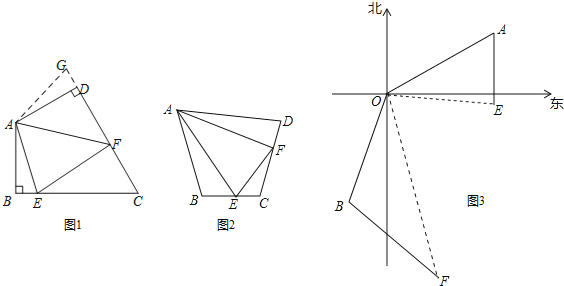
����Ŀ�������ⱳ������ͼ1�����ı���ABCD�У�AB��AD����BAD��120�㣬��B����ADC��90�㣬�ҡ�EAF��60�㣬̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ�ķ����ǽ���ABE�Ƶ�A��ʱ����ת120�㵽��ADG��λ�ã�Ȼ����֤����AFE �ա�AFG���Ӷ��ó�ʲô������
��̽�����죩��ͼ2�������ı���ABCD�У�AB��AD����B����D��180�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
������Ӧ�ã���ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��60���A������ͧ����ָ��������ƫ��20���B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ�������Ϸ�����30����/Сʱ���ٶ�ǰ������ͧ������ƫ��40��ķ�����50����/Сʱ���ٶ�ǰ����1Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������ͧ��ָ������O֮��нǡ�EOF��70�㣬�����ʱ����֮ͧ��ľ��룮
���𰸡�(1) ![]() (2)
(2) ![]() (3) ��ʱ����֮ͧ��ľ���Ϊ180���
(3) ��ʱ����֮ͧ��ľ���Ϊ180���
��������
�������ⱳ��������ABE�Ƶ�A��ʱ����ת120������ADG��λ�ú�AE=AG��DG=BE����EAF����FAG=60��������SAS֤����AFE �ա�AFG���ɵó����ۣ�̽�����죺�ӳ�FD����G��ʹDG��BE������AG��ͨ��SAS��֤����ABE�ա�ADG����AE��AG����BAE����DAG����EAF����FAG=60����������AEF�ա�AGF��EF=FG������FG��DG��DF��BE��DF����EF��BE��FD��Ȼ����������Ӧ�ã�����EF���ߡ�AOB��140������FOE��70����![]() ��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪAE=80��FB=100�����������ʱ����֮ͧ��ľ���EF��
��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪAE=80��FB=100�����������ʱ����֮ͧ��ľ���EF��
������������ⱳ��������ABE�Ƶ�A��ʱ����ת120������ADG��λ�ú�AE=AG��DG=BE����BAE����DAG����EAF��60������EAG��120����������FAG=60������EAG����FAG��������AFE �ա�AFG��SAS���� ��EF=FG����FG��DG��DF������EF��BE��FD��̽�����죺EF��BE��FD��Ȼ�������ӳ�FD����G��ʹDG��BE������AG����ΪAB=AD����B����ADG��90����������ABE�ա�ADG������ ��AE��AG����BAE����DAG��������EAG����FAG=60����������AEF�ա�AGF��SAS������EF=FG������FG��DG��DF��BE��DF����EF��BE��FD������Ӧ�ã�����EF���ߡ�AOB��30����90����20����140������FOE��70����![]() ��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪBF=50��2=100��AE=40��2=80�� ���Դ�ʱ����֮ͧ��ľ���EF��AE��FB=80+100=180�������ʱ����֮ͧ��ľ���Ϊ180���
��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪBF=50��2=100��AE=40��2=80�� ���Դ�ʱ����֮ͧ��ľ���EF��AE��FB=80+100=180�������ʱ����֮ͧ��ľ���Ϊ180���


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,BD�ǡ�ABCƽ���ߣ�DE![]() AB��E��AB=36cm,BC=24cm,S��ABC =144cm2,��DE�ij��ǣ� ��
AB��E��AB=36cm,BC=24cm,S��ABC =144cm2,��DE�ij��ǣ� ��

A. 4.8cm B. 4.5cm C. 4 cm D. 2.4cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ�����ε������߳��������ܹ���ֱ�������ε���( )
A. 1�� ![]() ��3 B.
��3 B. ![]() ��
�� ![]() ��5 C. 1.5��2��2.5 D.
��5 C. 1.5��2��2.5 D. ![]() ��
�� ![]() ��
�� ![]()
���𰸡�C
��������A��12+��![]() ��2��32�����ܹ���ֱ�������Σ���ѡ�����
��2��32�����ܹ���ֱ�������Σ���ѡ�����
B��(![]() 2+��
2+��![]() ��2��52�����ܹ���ֱ�������Σ���ѡ�����
��2��52�����ܹ���ֱ�������Σ���ѡ�����
C��1.52+22=2.52���ܹ���ֱ�������Σ���ѡ����ȷ��
D����![]() ����2+��
����2+��![]() ��2����
��2����![]() ��2�����ܹ���ֱ�������Σ���ѡ�����
��2�����ܹ���ֱ�������Σ���ѡ�����
��ѡ��C��
�����͡���ѡ��
��������
3
����Ŀ����Rt��ABC�У���C=90����AC=9��BC=12�����C��б��AB�ľ������� ��
��A��![]() ��B��
��B��![]() ��C��9 ��D��6
��C��9 ��D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ƻ��ӹ�360����������ڼ����ϵĸĽ�������˹���Ч�ʣ�ÿ���ԭ�ƻ���ӹ�20%�������ǰ10�����������ԭ�ƻ�ÿ���ܼӹ����ٸ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�G��BD��һ�㣬����CG���ӳ���BA���ӳ����ڵ�F����AD�ڵ�E��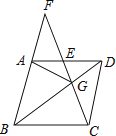
��1����֤��AG=CG��
��2����֤��AG2=GEGF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���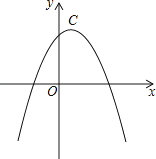
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ��
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�50ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������3��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=9��AD=4��EΪCD����һ�㣬CE=6����P�ӵ�B��������ÿ��1����λ���ٶ����ű�BA���յ�A�˶�������PE�����P�˶���ʱ��Ϊt�룮
��1�����ADE���ܳ���
��2����tΪ��ֵʱ����PAEΪֱ�������Σ�
��3���Ƿ����������t��ʹEAǡ��ƽ�֡�PED�������ڣ����t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com