
【题目】某车间计划加工360个零件,由于技术上的改进,提高了工作效率,每天比原计划多加工20%,结果提前10天完成任务,求原计划每天能加工多少个零件?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
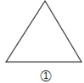
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.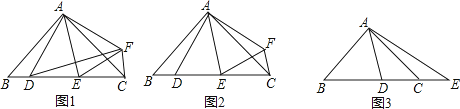
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
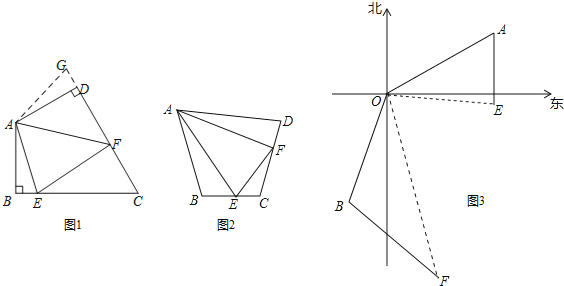
【题目】(问题背景)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE ≌△AFG,从而得出什么结论.
(探索延伸)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
(结论应用)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏东60°的A处,舰艇乙在指挥中心南偏西20°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正南方向以30海里/小时的速度前进,舰艇乙沿南偏东40°的方向以50海里/小时的速度前进,1小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题: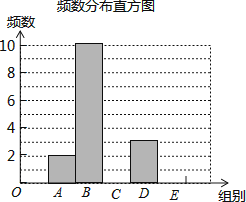
(1)填空:m= , n=
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com