
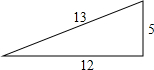
 如图,为一个直角三角形纸片,三条边长分别为5,12,13.将纸片折一下,使得短直角边重合到斜边上.折后没有被盖住部分的面积为________.
如图,为一个直角三角形纸片,三条边长分别为5,12,13.将纸片折一下,使得短直角边重合到斜边上.折后没有被盖住部分的面积为________.
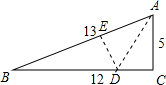 ∠C=90°,AC=5,BC=12,AB=13,
∠C=90°,AC=5,BC=12,AB=13, ,
, BE•DE=
BE•DE= ×8×
×8× =
= ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 底边 |
| 腰 |
| BC |
| AB |
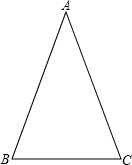 互唯一确定的.
互唯一确定的.| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
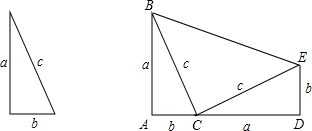 (1)如图,它可以看作是边长为a,b,c的两直角三角形成,其中A,B,C三点在同直线上,请从面积出发,写出一个a,b,c的等式;(要过程)
(1)如图,它可以看作是边长为a,b,c的两直角三角形成,其中A,B,C三点在同直线上,请从面积出发,写出一个a,b,c的等式;(要过程)查看答案和解析>>
科目:初中数学 来源:2011年福建省泉州市洛江区初二上学期期末数学卷 题型:选择题
如图1,是我国古代数学家赵爽的《勾股弦方图》,它是由四个全等的直角三角
形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的
面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2值为 ( )

A. 169 B. 25 C. 19 D. 13
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河北省曙光教育集团初三上学期中数学卷 题型:选择题
如图1,是我国古代数学家赵爽的《勾股弦方图》,它是由四个全等的直角三角
形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的
面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2值为 ( )

A. 169 B. 25 C. 19 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点A,点B,动点P
轴分别交于点A,点B,动点P![]() 在第一象限内,由点P向
在第一象限内,由点P向![]() 轴,
轴,![]() 轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P
轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P![]() 运动时,矩形PMON的面积为定值2.
运动时,矩形PMON的面积为定值2.
(1)求![]() 的度数;
的度数;
(2)求证:△![]() ∽△
∽△![]() ;
;
(3)当点E,F都在线段AB上时,由三条线段
AE,EF,BF组成一个三角形,记此三角
形的外接圆面积为![]() ,△
,△![]() 的面积为
的面积为![]() .
.
试探究:![]() 是否存在最小值?若存在,
是否存在最小值?若存在,
请求出该最小值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com