
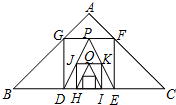
 如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )| A. | $\frac{2}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^{n-1}}$ | C. | $\frac{2}{3}•{(\frac{1}{2})^n}$ | D. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^n}$ |
分析 首先根据勾股定理得出BC的长,进而利用等腰直角三角形的性质得出DE的长,再利用锐角三角函数的关系得出$\frac{EI}{KI}$=$\frac{PF}{EF}$=$\frac{1}{2}$,即可得出正方形边长之间的变化规律,得出答案即可.
解答 解:∵在Rt△ABC中,AB=AC=2,
∴∠B=∠C=45°,BC=2$\sqrt{2}$,
∵在△ABC内作第一个内接正方形DEFG;
∴EF=EC=DG=BD,
∴DE=$\frac{1}{3}$BC,
∴DE=$\frac{2\sqrt{2}}{3}$,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,
∴$\frac{EI}{KI}$=$\frac{PF}{EF}$=$\frac{1}{2}$,
∴EI=$\frac{1}{2}$KI=$\frac{1}{2}$HI,
∵DH=EI,
∴HI=$\frac{1}{2}$DE=($\frac{1}{2}$)2-1×$\frac{2\sqrt{2}}{3}$,
则第n个内接正方形的边长为:$\frac{2\sqrt{2}}{3}$×($\frac{1}{2}$)n-1.
故选:B.
点评 此题主要考查了正方形的性质以及数字变化规律和勾股定理等知识,根据已知得出正方形边长的变化规律是解题关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
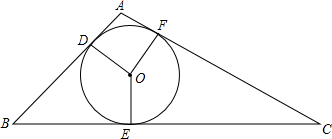 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{1}{2}$ | B. | m<2 | C. | m<$\frac{1}{2}$ | D. | m>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
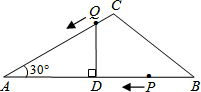 如图,在△ABC中,∠A=30°,AB=24,AC=16,点P从点B出发,沿BA边以4m/秒的速度移动到点A;点Q从点C出发,沿CA边以2/秒的速度向点A移动.P、Q两点同时出发,设运动的时间为t秒.
如图,在△ABC中,∠A=30°,AB=24,AC=16,点P从点B出发,沿BA边以4m/秒的速度移动到点A;点Q从点C出发,沿CA边以2/秒的速度向点A移动.P、Q两点同时出发,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com