
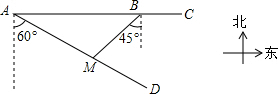
分析 根据题意,在△ABM中,∠BAM=30°,∠ABM=45°,AB=300($\sqrt{3}$+l)米.过点M作MN⊥AB于N,设MN=x米,用含x的代数式分别表示AN,BN,根据AN+BN=AB建立方程,解方程求出x的值,进而求出MA与MB的长.
解答 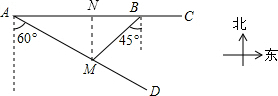 解:过点M作MN⊥AB于N,设MN=x米.
解:过点M作MN⊥AB于N,设MN=x米.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,
∴MA=2MN=2x,AN=$\sqrt{3}$MN=$\sqrt{3}$x.
在Rt△BMN中,∵∠BNM=90°,∠MBN=45°,
∴BN=MN=x,MB=$\sqrt{2}$MN=$\sqrt{2}$x.
∵AN+BN=AB,
∴$\sqrt{3}$x+x=300($\sqrt{3}$+l),
∴x=300,
∴MA=2x=600,MB=$\sqrt{2}$x=300$\sqrt{2}$.
故供水站M到小区A的距离是600米,到小区B的距离是300$\sqrt{2}$米.
点评 本题考查了解直角三角形的应用-方向角问题,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{5}$ | B. | b2•b3=b6 | C. | 4a-9a=-5 | D. | (ab2)2=a2b4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32 | B. | 29 | C. | 28 | D. | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com