
分析 首先去掉括号,然后根据加法交换律和结合律,求出算式2($\sqrt{2}$-$\sqrt{2}$÷4)+($\sqrt{2}$-2)-(2$\sqrt{2}$-3)的值是多少即可.
解答 解:2($\sqrt{2}$-$\sqrt{2}$÷4)+($\sqrt{2}$-2)-(2$\sqrt{2}$-3)
=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-2-2$\sqrt{2}$+3
=(2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-2$\sqrt{2}$)+(3-2)
=$\frac{\sqrt{2}}{2}+1$
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
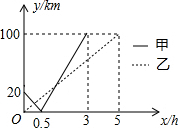 有甲、乙两军舰在南海执行任务.它们分别从A,B两处沿直线同时匀速前往C处,最终到达C处(A,B,C,三处顺次在同一直线上).设甲、乙两军舰行驶x(h)后,与B处相距的距离分别是y1(海里)和y2(海里),y1,y2与x的函数关系如图所示
有甲、乙两军舰在南海执行任务.它们分别从A,B两处沿直线同时匀速前往C处,最终到达C处(A,B,C,三处顺次在同一直线上).设甲、乙两军舰行驶x(h)后,与B处相距的距离分别是y1(海里)和y2(海里),y1,y2与x的函数关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
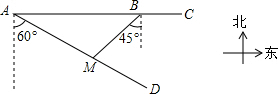
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b | B. | a<3 | C. | b<3 | D. | c<-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com