
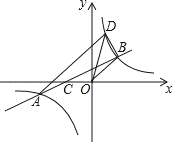
【题目】如图,点A和点B分别是反比例函数y=![]() (k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=
(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=![]() ,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=
,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=![]() 于点D,连接OD,BD.
于点D,连接OD,BD.
(1)求点A的坐标;
(2)求△OBD的面积.
【答案】(1) 点A的坐标为(﹣4,﹣1).(2)3.
【解析】
(1)过点B作BE⊥x轴于点E,根据∠BOC=135°可得出∠BOE=45°,从而得出OE=BE,再根据tan∠BCO=![]() 且CO=2,可得出点B坐标为(2,2),以及反比例函数系数k的几何意义即可得出反比例函数解析式,由B、C点的坐标利用待定系数法即可求出直线AB的函数解析式,将直线AB的函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,解方程即可求出点A的横坐标,将其代入反比例函数解析式中即可得出结论;
且CO=2,可得出点B坐标为(2,2),以及反比例函数系数k的几何意义即可得出反比例函数解析式,由B、C点的坐标利用待定系数法即可求出直线AB的函数解析式,将直线AB的函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,解方程即可求出点A的横坐标,将其代入反比例函数解析式中即可得出结论;
(2)设直线AD与y轴交于点M,连接BM,则S△BOD=S△BOM,根据OB的解析式、AD∥OB及点A的坐标可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点M的坐标,再利用三角形的面积公式即可求出结论.
解:(1)过点B作BE⊥x轴于点E,如图1所示.
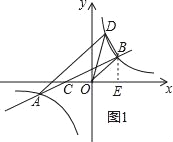
∵∠BOC=135°,
∴∠BOE=45°,
∴OE=BE.
又∵tan∠BCO=![]() =
=![]() ,OC=2,
,OC=2,
∴BE=OE=2,
∴点B的坐标为(2,2).
∴k=2×2=4,
即反比例函数的解析式为y=![]() .
.
设直线AB的解析式为y=ax+b,
将点B(2,2)、点C(﹣2,0)代入到y=ax+b中,
得![]() ,解得:
,解得: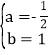 .
.
∴直线AB的解析式为y=![]() x+1.
x+1.
将y=![]() x+1代入到y=
x+1代入到y=![]() 中,
中,
得![]() =
=![]() x+1,即x2+2x﹣8=0,
x+1,即x2+2x﹣8=0,
解得:x1=﹣4,x2=2.
当x=﹣4时,y=![]() =﹣1.
=﹣1.
∴点A的坐标为(﹣4,﹣1).
(2)设直线AD与y轴交于点M,连接BM,如图2所示.
∵AD∥BO,
∴设直线AD的解析式为y=x+c,
∵点A(﹣4,﹣1)在直线AD的图象上,
∴﹣1=﹣4+c,解得:c=3.
∴直线AD的解析式为y=x+3.
当x=0时,y=x+3=3,
∴点M的坐标为(0,3).
∵AD∥BO,
∴S△BOD=S△BOM=![]() OMxB=
OMxB=![]() ×3×2=3.
×3×2=3.


科目:初中数学 来源: 题型:
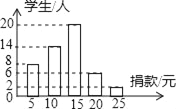
【题目】在一次捐款活动中,学校团支书想了解本校学生的捐款情况,随机抽取了50名学生的捐款进行了统计,并绘制成如图所示的统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)如果捐款的学生有300人,估计这次捐款有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 的图象上位于直线
的图象上位于直线![]() 下方的点,过点
下方的点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() ,交直线
,交直线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年的暑假,李刚和他的父母计划去新疆旅游,他们打算坐飞机到乌鲁木齐,第二天租用一辆汽车自驾出游.

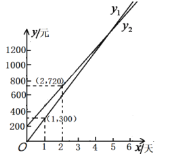
根据以上信息,解答下列问题:
(1)设租车时间为![]() 天,租用甲公司的车所需费用为
天,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助李刚,选择租用哪个公司的车自驾出游比较合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
如图1,已知△ABC中,AD 为中线.延长AD至点E,使 DE=AD.在△ADC和△EDB中,AD=DE,∠ADC=∠EDB,BD=CD,所以,△ACD≌△EBD,进一步可得到AC=BE,AC//BE等结论.
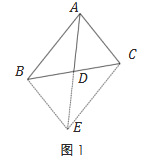
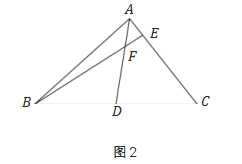
在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.
解决问题:如图2,在△ABC中,AD是三角形的中线,点F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com