
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßÓėxÖį½»ÓŚA£Øx1 £¬ 0£©”¢B£Øx2 £¬ 0£©Į½µć£¬ĒŅx1£¼x2 £¬ ÓėyÖį½»ÓŚµćC£Ø0£¬©4£©£¬ĘäÖŠx1 £¬ x2ŹĒ·½³Ģx2©4x©12=0µÄĮ½øöøł£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćMŹĒĻ߶ĪABÉĻµÄŅ»øö¶Æµć£¬¹żµćM×÷MN”ĪBC£¬½»ACÓŚµćN£¬Į¬½ÓCM£¬µ±”÷CMNµÄĆ껿×ī“óŹ±£¬ĒóµćMµÄ×ų±ź£»
£Ø3£©µćD£Ø4£¬k£©ŌŚ£Ø1£©ÖŠÅ×ĪļĻßÉĻ£¬µćEĪŖÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŌŚxÖįÉĻŹĒ·ń“ęŌŚµćF£¬Ź¹ŅŌA”¢D”¢E”¢FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚ£¬Ēó³öĖłÓŠĀś×ćĢõ¼žµÄµćFµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ”ßx2©4x©12=0£¬
”ąx1=©2£¬x2=6£®
”ąA£Ø©2£¬0£©£¬B£Ø6£¬0£©£¬
ÓÖ”ßÅ×ĪļĻß¹żµćA”¢B”¢C£¬¹ŹÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=a£Øx+2£©£Øx©6£©£¬
½«µćCµÄ×ų±ź“śČė£¬ĒóµĆ ![]() £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖ ![]() £»
£»
£Ø2£©
½ā£ŗÉčµćMµÄ×ų±źĪŖ£Øm£¬0£©£¬¹żµćN×÷NH”ĶxÖįÓŚµćH£ØČēĶ¼£Ø1£©£©£®
”ßµćAµÄ×ų±źĪŖ£Ø©2£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø6£¬0£©£¬
”ąAB=8£¬AM=m+2£¬
”ßMN”ĪBC£¬”ą”÷MNA”×”÷BCA£®
”ą ![]() £¬
£¬
”ą ![]() £¬
£¬
”ą ![]() £¬
£¬
”ą ![]() £¬
£¬
= ![]() £¬
£¬
= ![]() £®
£®
”ąµ±m=2Ź±£¬S”÷CMNÓŠ×ī“óÖµ4£®
“ĖŹ±£¬µćMµÄ×ų±źĪŖ£Ø2£¬0£©£»

£Ø3£©
½ā£ŗ”ßµćD£Ø4£¬k£©ŌŚÅ×ĪļĻß ![]() ÉĻ£¬
ÉĻ£¬
”ąµ±x=4Ź±£¬k=©4£¬
”ąµćDµÄ×ų±źŹĒ£Ø4£¬©4£©£®
¢ŁČēĶ¼£Ø2£©£¬µ±AFĪŖĘ½ŠŠĖıߊĪµÄ±ßŹ±£¬AFĘ½ŠŠĒŅµČÓŚDE£¬

”ßD£Ø4£¬©4£©£¬”ąDE=4£®
”ąF1£Ø©6£¬0£©£¬F2£Ø2£¬0£©£¬
¢ŚČēĶ¼£Ø3£©£¬µ±AFĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߏ±£¬ÉčF£Øn£¬0£©£¬

”ßµćAµÄ×ų±źĪŖ£Ø©2£¬0£©£¬
ŌņĘ½ŠŠĖıߊĪµÄ¶Ō³ĘÖŠŠÄµÄŗį×ų±źĪŖ£ŗ ![]() £¬
£¬
”ąĘ½ŠŠĖıߊĪµÄ¶Ō³ĘÖŠŠÄ×ų±źĪŖ£Ø ![]() £¬0£©£¬
£¬0£©£¬
”ßD£Ø4£¬©4£©£¬
”ąE'µÄŗį×ų±źĪŖ£ŗ ![]() ©4+
©4+ ![]() =n©6£¬
=n©6£¬
E'µÄׯ×ų±źĪŖ£ŗ4£¬
”ąE'µÄ×ų±źĪŖ£Øn©6£¬4£©£®
°ŃE'£Øn©6£¬4£©“śČė ![]() £¬µĆn2©16n+36=0£®
£¬µĆn2©16n+36=0£®
½āµĆ ![]() £®
£® ![]() £¬
£¬ ![]() £¬
£¬
×ŪÉĻĖłŹöF1£Ø©6£¬0£©£¬F2£Ø2£¬0£©£¬F3£Ø8©2 ![]() £¬0£©£¬F4£Ø8+2
£¬0£©£¬F4£Ø8+2 ![]() £¬0£©£®
£¬0£©£®
”¾½āĪö”æ£Ø1£©øł¾ŻŅ»ŌŖ¶ž“Ī·½³Ģ½ā·ØµĆ³öA£¬BĮ½µćµÄ×ų±ź£¬ŌŁĄūÓĆ½»µćŹ½Ēó³ö¶ž“ĪŗÆŹż½āĪöŹ½£»£Ø2£©Ź×ĻČÅŠ¶Ø”÷MNA”×”÷BCA£®µĆ³ö ![]() £¬½ų¶ųµĆ³öŗÆŹżµÄ×īÖµ£»£Ø3£©·Ö±šøł¾Żµ±AFĪŖĘ½ŠŠĖıߊĪµÄ±ßŹ±£¬AFĘ½ŠŠĒŅµČÓŚDEÓėµ±AFĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߏ±£¬·ÖĪöµĆ³ö·ūŗĻŅŖĒóµÄ“š°ø£®
£¬½ų¶ųµĆ³öŗÆŹżµÄ×īÖµ£»£Ø3£©·Ö±šøł¾Żµ±AFĪŖĘ½ŠŠĖıߊĪµÄ±ßŹ±£¬AFĘ½ŠŠĒŅµČÓŚDEÓėµ±AFĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߏ±£¬·ÖĪöµĆ³ö·ūŗĻŅŖĒóµÄ“š°ø£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖABĪŖ”ŃOÖ±¾¶£¬ŅŌOAĪŖÖ±¾¶×÷”ŃM£®¹żB×÷”ŃMµĆĒŠĻßBC£¬ĒŠµćĪŖC£¬½»”ŃOÓŚE£® 
£Ø1£©ŌŚĶ¼ÖŠ¹żµćB×÷”ŃM×÷ĮķŅ»ĢõĒŠĻßBD£¬ĒŠµćĪŖµćD£ØÓĆ³ß¹ę×÷Ķ¼£¬±£Įō×÷Ķ¼ŗŪ¼££¬²»Š“×÷·Ø£¬²»ÓĆÖ¤Ć÷£©£»
£Ø2£©Ö¤Ć÷£ŗ”ĻEAC=”ĻOCB£»
£Ø3£©ČōAB=4£¬ŌŚĶ¼2ÖŠ¹żO×÷OP”ĶAB½»”ŃOÓŚP£¬½»”ŃMµÄĒŠĻßBDÓŚN£¬ĒóBNµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AD”ĪBC£¬”ĻC=90”ć£¬EĪŖCDÉĻŅ»µć£¬·Ö±šŅŌEA£¬EBĪŖÕŪŗŪ½«Į½øö½Ē£Ø”ĻD£¬”ĻC£©ĻņÄŚÕŪµž£¬µćC£¬DĒ”ŗĆĀäŌŚAB±ßµÄµćF“¦£®ČōAD=2£¬BC=3£¬ŌņEFµÄ³¤ĪŖ £® 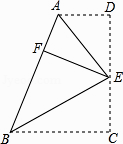
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy=©x2+2x¾¹żŌµćO£¬ĒŅÓėÖ±Ļßy=x©2½»ÓŚB£¬CĮ½µć£®
£Ø1£©ĒóÅ×ĪļĻߵĶ„µćAµÄ×ų±ź¼°µćB£¬CµÄ×ų±ź£»
£Ø2£©ĒóÖ¤£ŗ”ĻABC=90”ć£»
£Ø3£©ŌŚÖ±ĻßBCÉĻ·½µÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PBCµÄĆ껿×ī“ó£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø4£©ČōµćNĪŖxÖįÉĻµÄŅ»øö¶Æµć£¬¹żµćN×÷MN”ĶxÖįÓėÅ×ĪļĻß½»ÓŚµćM£¬ŌņŹĒ·ń“ęŌŚŅŌO£¬M£¬NĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öµćNµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒ±ß³¤ĪŖ2µÄÕż·½ŠĪ£¬µćGŹĒBCŃÓ³¤ĻßÉĻŅ»µć£¬Į¬½ÓAG£¬µćE”¢F·Ö±šŌŚAGÉĻ£¬Į¬½ÓBE”¢DF£¬”Ļ1=”Ļ2£¬”Ļ3=”Ļ4£® 
£Ø1£©Ö¤Ć÷£ŗ”÷ABE”Õ”÷DAF£»
£Ø2£©Čō”ĻAGB=30”ć£¬ĒóEFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬“óĀ„ABÓŅ²ąÓŠŅ»ÕĻ°Īļ£¬ŌŚÕĻ°ĪļµÄÅŌ±ßÓŠŅ»“±Š”Ā„DE£¬ŌŚŠ”Ā„µÄ¶„¶ĖD“¦²āµĆÕĻ°Īļ±ßŌµµćCµÄø©½ĒĪŖ30”ć£¬²āµĆ“óĀ„¶„¶ĖAµÄŃö½ĒĪŖ45”ć£ØµćB£¬C£¬EŌŚĶ¬Ņ»Ė®Ę½Ö±ĻßÉĻ£©£¬ŅŃÖŖAB=80m£¬DE=10m£¬ĒóÕĻ°ĪļB£¬CĮ½µć¼äµÄ¾ąĄė£Ø½į¹ū¾«Č·µ½0.1m£©£Ø²Īæ¼Źż¾Ż£ŗ ![]() ”Ö1.414£¬
”Ö1.414£¬ ![]() ”Ö1.732£©
”Ö1.732£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻA=90”ć£¬BC=4£¬µćPŹĒ”÷ABC±ßÉĻŅ»¶Æµć£¬ŃŲB”śA”śCµÄĀ·¾¶ŅĘ¶Æ£¬¹żµćP×÷PD”ĶBCÓŚµćD£¬ÉčBD=x£¬”÷BDPµÄĆ껿ĪŖy£¬ŌņĻĀĮŠÄÜ“óÖĀ·“Ó³yÓėxŗÆŹż¹ŲĻµµÄĶ¼ĻóŹĒ£Ø £©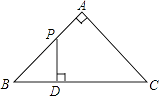
A.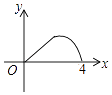
B.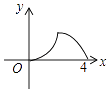
C.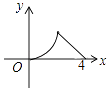
D.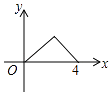
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŅŃÖŖ¾ŲŠĪABCDÖŠ£¬AB=60cm£¬BC=90cm£®µćP“ÓµćA³ö·¢£¬ŅŌ3cm/sµÄĖŁ¶ČŃŲABŌĖ¶Æ£ŗĶ¬Ź±£¬µćQ“ÓµćB³ö·¢£¬ŅŌ20cm/sµÄĖŁ¶ČŃŲBCŌĖ¶Æ£®µ±µćQµ½“ļµćCŹ±£¬P”¢QĮ½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćP”¢QŌĖ¶ÆµÄŹ±¼äĪŖt£Øs£©£®
£Ø1£©µ±t=sŹ±£¬”÷BPQĪŖµČŃüČż½ĒŠĪ£»
£Ø2£©µ±BDĘ½·ÖPQŹ±£¬ĒótµÄÖµ£»
£Ø3£©ČēĶ¼¢Ś£¬½«”÷BPQŃŲPQÕŪµž£¬µćBµÄ¶ŌÓ¦µćĪŖE£¬PE”¢QE·Ö±šÓėAD½»ÓŚµćF”¢G£®Ģ½Ė÷£ŗŹĒ·ń“ęŌŚŹµŹżt£¬Ź¹µĆAF=EF£æČē¹ū“ęŌŚ£¬Ēó³ötµÄÖµ£ŗČē¹ū²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=x2©2x©3£¬µćPŌŚøĆŗÆŹżµÄĶ¼ĻóÉĻ£¬µćPµ½xÖį”¢yÖįµÄ¾ąĄė·Ö±šĪŖd1”¢d2 £® Éčd=d1+d2 £¬ ĻĀĮŠ½įĀŪÖŠ£ŗ
¢Łdƻӊ×ī“óÖµ£»
¢Śdƻӊ×īŠ”Öµ£»
¢Ū©1£¼x£¼3Ź±£¬dĖęxµÄŌö“ó¶ųŌö“ó£»
¢ÜĀś×ćd=5µÄµćPÓŠĖÄøö£®
ĘäÖŠÕżČ·½įĀŪµÄøöŹżÓŠ£Ø £©
A.1øö
B.2øö
C.3øö
D.4øö
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com