
| A. | 在一次抽奖活动中,“中奖的概率是$\frac{1}{100}$”表示抽奖l00次就一定会中奖 | |
| B. | 某市“明天降雨的概率是75%”表示明天有75%的时间会降雨 | |
| C. | 随机抛掷一枚均匀的硬币,落地后正面一定朝上 | |
| D. | 在平面内,平行四边形的两条对角线一定相交 |
分析 根据概率的意义和必然发生的事件的概率P(A)=1、不可能发生事件的概率P(A)=0对A、B、C、D进行判定.
解答 解:A、在一次抽奖活动中,“中奖的概率是$\frac{1}{100}$”表示抽奖l00次就可能会中奖,故A不符合题意;
B、某市“明天降雨的概率是75%”表示明天降雨的可能性大,故B不符合题意;
C、随机抛掷一枚均匀的硬币,落地后正面可能朝上,故C不符合题意;
D、在平面内,平行四边形的两条对角线一定相交,故D符合题意;
故选:D.
点评 本题考查了概率的意义:一般地,在大量重复实验中,如果事件A发生的频率mn会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P(A)=p;概率是频率(多个)的波动稳定值,是对事件发生可能性大小的量的表现.必然发生的事件的概率P(A)=1;不可能发生事件的概率P(A)=0.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
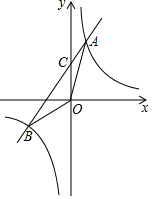 如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:
如图,已知反比例函数y=$\frac{8}{x}$与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是-2.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com