练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一幅长8分米，宽6分米的矩形风景画（如图①）的四周镶宽度相同的金色纸边，制成一幅矩形挂图（如图②）．如果要使整个挂图的面积是80平方分米，求金色纸边的宽．


    解：设金色纸边的宽为x分米 ．    分

    根据题意，得         

    （2x＋6）(2x＋8)＝80.            

    解得：x1＝1，x2＝－8（不合题意，舍去）．     

    答：金色纸边的宽为1分米．                               


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    八年级学生小明是一个喜欢思考问题而又乐于助人的好学生，一天邻居家读小学的小李，请他帮忙检查作业：

    7×9＝63；8×8＝64；

    11×13＝143；12×12＝144；

    24×26＝624；25×25＝625.

    小明仔细检查后，夸小李聪明，作业全对了！小明还从这几题中发现了一个规律，你知道小明发现了什么规律吗？请用字母表示这一规律，并说明它的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在四边形ABCD中，∠A＝45°，∠C＝90°，∠ABD＝75°，∠DBC＝30°，AB＝．求BC的长．

    解：



    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD中，AB＝8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动．设运动时间为t(s)，△OEF的面积为S(cm2)，则S(cm2)与t(s)的函数关系可用图象表示为

     


    A                 B                C                  D

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平行四边形ABCD中，E为CD上一点，连结AE，BD，且AE，BD交于点F，S△DEF∶S△ABF = 4∶25，求DE∶EC的值．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系xOy中，二次函数的图象与x轴负半轴交于点A，与y轴交于点B（0，4），已知点E（0，1）．

    （1）求m的值及点A的坐标；

    （2）如图，将△AEO沿x轴向右平移得到△A′E′O′，连结A′B、BE′．

    ①当点E′落在该二次函数的图象上时，求AA′的长；

    ②设AA′=n，其中0＜n＜2，试用含n的式子表示A′B2+BE′2，并求出使A′B2+BE′2取得最小值时点E′的坐标；

    ③当A′B+BE′取得最小值时，求点E′的坐标．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图，是⊙的切线， 为切点，的延长线交⊙于点，连接，若，，则等于(    ) A. 4      B.6  C.        D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


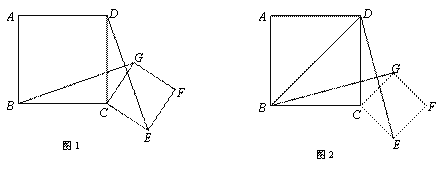
    已知四边形ABCD和四边形CEFG都是正方形 ，且AB>CE．

    （1）如图1，连接BG、DE．求证：BG=DE；

    （2）如图2，如果正方形ABCD的边长为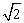，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD，BG=BD.

    ①求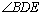的度数；

    ②请直接写出正方形CEFG的边长的值.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在梯形ABCD中，AB∥DC，∠A＝90°，点P在AD边上，且．若AB＝6，DC＝4，PD＝2，求PB的长．

    查看答案和解析>>

    同步练习册答案