10.观察下列分母有理化运算:$\frac{1}{{1+\sqrt{2}}}=-1+\sqrt{2}$,$\frac{1}{{\sqrt{2}+\sqrt{3}}}=-\sqrt{2}+\sqrt{3}$,$\frac{1}{{\sqrt{3}+\sqrt{4}}}=-\sqrt{3}+\sqrt{4}$利用上面的规律计算:($\frac{1}{{1+\sqrt{2}}}+\frac{1}{{\sqrt{2}+\sqrt{3}}}+\frac{1}{{\sqrt{3}+\sqrt{4}}}+…$+$\frac{1}{{\sqrt{2001}+\sqrt{2002}}}+\frac{1}{{\sqrt{2002}+\sqrt{2003}}}$)(1+$\sqrt{2003}$)=2002.
分析 原式第一个括号中各项分母有理化,计算即可得到结果.
解答 解:原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2002}$-$\sqrt{2001}$+$\sqrt{2003}$-$\sqrt{2002}$)(1+$\sqrt{2003}$)=($\sqrt{2003}$-1)(1+$\sqrt{2003}$)=2003-1=2002.
故答案为:2002.
点评 此题考查了分母有理化,找有理化因式的方法为:正确选择两个二次根式,使它们的积符合平方差公式.

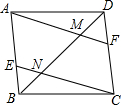 如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.
如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.