
 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )| A. | 8cm | B. | $\sqrt{91}$cm | C. | 6cm | D. | 2cm |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
 如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,1) | B. | (4,-1) | C. | (-4,-1) | D. | (-4,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )| A. | 4<m<8+$\sqrt{7}$ | B. | 4-$\sqrt{7}$<m<5 | C. | 5<m<9 | D. | 5<m<4+$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
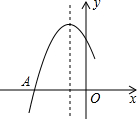 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数的绝对值一定是正数 | |
| B. | 有理数的绝对值一定是非负数 | |
| C. | 绝对值等于本身的数一定是正数 | |
| D. | 如果两个数的绝对值相等,那么这两个数相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com