
如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.

科目:初中数学 来源:2013-2014学年山东省初中学业水平考试数学模拟试卷(解析版) 题型:选择题
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为

A.4 B.6 C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:解答题
(1)如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.
(2)如图,在梯形ABCD中,AD∥BC,∠B =90°,AD=2,BC =5,tanC = ,求腰AB的长.
,求腰AB的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:解答题
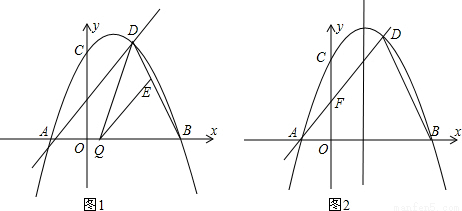
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m),
(1)求二次函数的解析式并写出D点坐标;
(2)点Q是线段AB上的一动点,过点Q作QE∥AD交BD于E,连结DQ,当△DQE的面积最大时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:填空题
如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m(结果不作近似计算).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
如图,数轴上A,B两点表示的数分别为-1和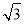 ,点B关于点A的对称点为C,则点C所表示的数为( )
,点B关于点A的对称点为C,则点C所表示的数为( )
A.-2-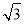 B.-1-
B.-1-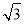 C.-2+
C.-2+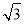 D.1+
D.1+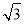

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
袋子中装有4个黑球2个白球,这些球除了颜色外都相同,从袋子中随机摸出一个球,则摸到黑球的概率是
A. B.
B.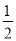 C.
C.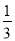 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com