
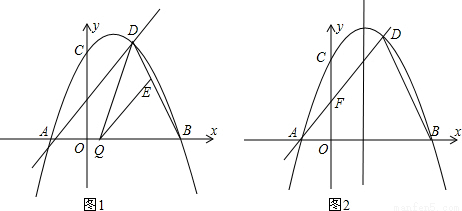
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m),
(1)求二次函数的解析式并写出D点坐标;
(2)点Q是线段AB上的一动点,过点Q作QE∥AD交BD于E,连结DQ,当△DQE的面积最大时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
(1)点D的坐标为(2,4).
(2)当t=1时,S△DQE有最大值,所以此时Q点的坐标为(1,0);
(3)满足条件的点N的坐标为N(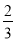 ,0),点M的坐标为M(1,1).
,0),点M的坐标为M(1,1).
【解析】
试题分析:(1)根据点C(0,4),点B(4,0),抛物线的对称轴为x=1可得关于a,b,c的方程组,解方程求得a,b,c的值,从而得到二次函数的解析式,再将点D(2,m)代入二次函数的解析式,得到关于m的方程,求得m的值,从而求解;
(2)先求得A,B点的坐标,过点E作EG⊥QB,根据相似三角形的判定和性质可得EG=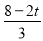 ,由于S△DQE=S△BDQ-S△BEQ,配方后即可得到S△DQE有最大值时Q点的坐标;
,由于S△DQE=S△BDQ-S△BEQ,配方后即可得到S△DQE有最大值时Q点的坐标;
(3)根据待定系数法得到直线AD的解析式为:y=x+2,过点F作关于x轴的对称点F′,即F′(0,-2),再连接DF′交对称轴于M′,x轴于N′,由条件可知,点C,D是关于对称轴x=1对称,则CF+F′N+M′N′+M′C=CF+DF′=2+2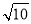 ,得到四边形CFNM的最短周长为:2+2
,得到四边形CFNM的最短周长为:2+2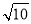 时直线DF′的解析式为:y=3x-2,长而得到满足条件的点M和点N的坐标.
时直线DF′的解析式为:y=3x-2,长而得到满足条件的点M和点N的坐标.
(1)由题意有: ,
,
解得: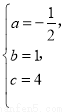 .
.
所以,二次函数的解析式为:y=- x2+x+4,
x2+x+4,
∵点D(2,m)在抛物线上,即m=- ×22+2+4=4,
×22+2+4=4,
所以点D的坐标为(2,4).
(2)令y=0,即- x2+x+4=0,解得:x1=4,x2=-2,
x2+x+4=0,解得:x1=4,x2=-2,
∴A,B点的坐标分别是(-2,0),(4,0),
如图1,过点E作EG⊥QB,垂足为G,设Q点坐标为(t,0),
∵QE∥AD,
∴△BEQ与△BDA相似,
∴ ,即
,即 ,
,
∴EG= ,
,
∴S△BEQ= ×(4-t)×
×(4-t)× ,
,
∴S△DQE=S△BDQ-S△BEQ
= ×(4-t)×4-S△BEQ
×(4-t)×4-S△BEQ
=2(4-t)- (4-t)2
(4-t)2
=- t2+
t2+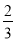 t+
t+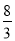
=- (t-1)2+3,
(t-1)2+3,
∴当t=1时,S△DQE有最大值,所以此时Q点的坐标为(1,0);

(3)由A(-2,0),D(2,4),可求得直线AD的解析式为:y=x+2,即点F的坐标为:F(0,2),
如图2,过点F作关于x轴的对称点F′,即F′(0,-2),再连接DF′交对称轴于M′,x轴于N′,由条件可知,点C,D是关于对称轴x=1对称,
则CF+F′N+M′N′+M′C=CF+DF′=2+2 ,
,
则四边形CFNM的周长=CF+FN+NM+MC≥CF+FN′+M′N′+M′C,
即四边形CFNM的最短周长为:2+2 .
.
此时直线DF′的解析式为:y=3x-2,
所以存在点N的坐标为N(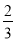 ,0),点M的坐标为M(1,1).
,0),点M的坐标为M(1,1).

考点:二次函数综合题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:2013-2014学年山东省初中学业水平考试数学模拟试卷(解析版) 题型:填空题
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画 ,连结AF、CF,则图中阴影部分面积为 .
,连结AF、CF,则图中阴影部分面积为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:解答题
如图1,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
(1)求抛物线的解析式;
(2)抛物线对称轴上有一动点P,当 时,求出点
时,求出点 的坐标;
的坐标;
(3)如图2所示,连结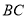 ,
, 是线段
是线段 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点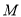 的横坐标为.当t为何值时,
的横坐标为.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
已知二次函数 的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
A.(1,0) B.(-1,0) C.(2,0) D.(-2,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
近年来,随着交通网络的不断完善,我市近郊游持续升温。 据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为
A. 人 B.
人 B. 人 C.
人 C. 人 D.
人 D.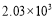 人
人
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB. 设 =k.
=k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?并说明理由。
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是

A.4 B.5 C.6 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com