
如图1,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
(1)求抛物线的解析式;
(2)抛物线对称轴上有一动点P,当 时,求出点
时,求出点 的坐标;
的坐标;
(3)如图2所示,连结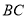 ,
, 是线段
是线段 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点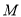 的横坐标为.当t为何值时,
的横坐标为.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?

(1) y=x2-3x+2;;(2)(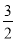 ,
,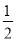 )或(
)或(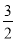 ,
,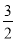 );(3)t=1时,S△BCN的最大值为1.
);(3)t=1时,S△BCN的最大值为1.
【解析】
试题分析:(1)已知了C点的坐标,即可得到OC的长,根据∠OAC的正切值即可求出OA的长,由此可得到A点的坐标,将A、C的坐标代入抛物线中,即可确定该二次函数的解析式;
(2)根据抛物线的解析式即可确定其对称轴方程,由此可得到点P的横坐标;若∠APC=90°,则∠PAE和∠CPD是同角的余角,因此两角相等,则它们的正切值也相等,由此可求出线段PE的长,即可得到点P点的坐标;(用相似三角形求解亦可)
(3)根据B、C的坐标易求得直线BC的解析式,已知了点M的横坐标为t,根据直线BC和抛物线的解析式,即可用t表示出M、N的纵坐标,由此可求得MN的长,以MN为底,B点横坐标的绝对值为高,即可求出△BNC的面积(或者理解为△BNC的面积是△CMN和△MNB的面积和),由此可得到关于S(△BNC的面积)、t的函数关系式,根据所得函数的性质即可求得S的最大值及对应的t的值.
试题解析:(1)∵抛物线y=x2+bx+c过点C(0,2),
∴c=2;
又∵tan∠OAC=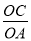 =2,
=2,
∴OA=1,即A(1,0);
又∵点A在抛物线y=x2+bx+2上,
∴0=12+b×1+2,b=-3;
∴抛物线对应的二次函数的解析式为y=x2-3x+2;
(2)存在.
过点C作对称轴l的垂线,垂足为D,如图所示,
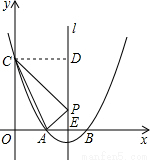
∴x=-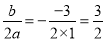 ;
;
∴AE=OE-OA=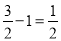 ,
,
∵∠APC=90°,
∴tan∠PAE=tan∠CPD,
∴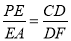 ,即
,即 ,
,
解得PE=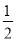 或PE=
或PE=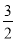 ,
,
∴点P的坐标为(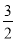 ,
,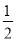 )或(
)或(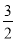 ,
, ).
).
(3)如图所示,易得直线BC的解析式为:y=-x+2,
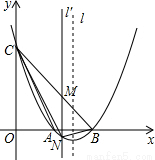
∵点M是直线l′和线段BC的交点,
∴M点的坐标为(t,-t+2)(0<t<2),
∴MN=-t+2-(t2-3t+2)=-t2+2t,
∴S△BCN=S△MNC+S△MNB=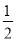 MN·t+
MN·t+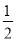 MN·(2-t),
MN·(2-t),
=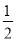 MN·(t+2-t)=MN=-t2+2t(0<t<2),
MN·(t+2-t)=MN=-t2+2t(0<t<2),
∴S△BCN=-t2+2t=-(t-1)2+1,
∴当t=1时,S△BCN的最大值为1.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年山东青岛平度古岘镇古岘中学九年级下学期阶段性质量检测数学试卷(解析版) 题型:解答题
学习了函数的知识后,数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现,每支定价3元,每天能卖出100支,而且每支定价每下降0.1元,其销售量将增加10支。但是物价局规定,该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元,每天的销售利润为y元。
(1)求每天的销售利润为y与每支定价x之间的函数关系式;
(2)如果要实现每天75元的销售利润,那么每支定价应为多少元?
(3)当每支定价为多少元时,可以使这种笔每天的销售利润最大?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省初中学业水平考试数学模拟试卷(解析版) 题型:选择题
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于

A.44° B.60° C.67° D.77°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:选择题
圆锥的高是4cm,母线长5cm,则其侧面展开图的面积为( )
A.30πcm2 B.24πcm2 C.15πcm2 D.18πcm2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:选择题
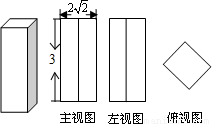
一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底面边长分别为( )
A.3,2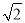 B.2,2
B.2,2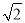 C.3,2 D.2,3
C.3,2 D.2,3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:解答题
(1)如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.
(2)如图,在梯形ABCD中,AD∥BC,∠B =90°,AD=2,BC =5,tanC = ,求腰AB的长.
,求腰AB的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:解答题
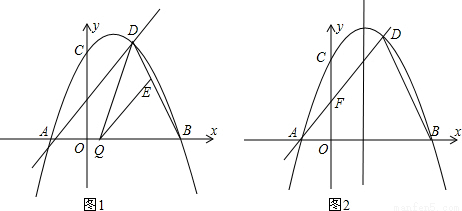
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m),
(1)求二次函数的解析式并写出D点坐标;
(2)点Q是线段AB上的一动点,过点Q作QE∥AD交BD于E,连结DQ,当△DQE的面积最大时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
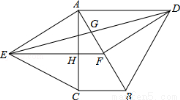
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD;其中正确结论的是( )
BD;其中正确结论的是( )
(A)①②③ (B)①②④ (C)①③④ (D)②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com