
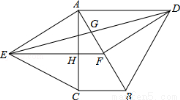
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD;其中正确结论的是( )
BD;其中正确结论的是( )
(A)①②③ (B)①②④ (C)①③④ (D)②③④
C.
【解析】
试题分析:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,

∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF= BC,
BC,
∵BC= AB,AB=BD,
AB,AB=BD,
∴HF= BD,故④说法正确;
BD,故④说法正确;

∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG= AF,
AF,
∴AG= AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故选C.
考点:1.菱形的判定;2.等边三角形的性质;3.含30度角的直角三角形


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:解答题
如图1,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
(1)求抛物线的解析式;
(2)抛物线对称轴上有一动点P,当 时,求出点
时,求出点 的坐标;
的坐标;
(3)如图2所示,连结 ,
, 是线段
是线段 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的横坐标为.当t为何值时,
的横坐标为.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB. 设 =k.
=k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?并说明理由。
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
(A) (B)
(B) (C)
(C)  (D)
(D)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
据统计,1959年南湖革命纪念馆成立以来,约有2500万人次参观了南湖红船(中共一大会址).数2500万用科学计数法表示为( )
(A)2.5×108 (B)2.5×107 (C)2.5×106 (D)25×106
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是

A.4 B.5 C.6 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com