
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.

【答案】(1)∠CDB=60°.(2)见解析
【解析】
(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CD=CB,△BCD是等边三角形,即可求解;
(2)先判断出∠CDE=∠ABC,进而得出△CDE≌△CBF(AAS),再根据分割面积法证明四边形ABCD的面积是定值即可.
(1)∵射线AC是∠MAN的角平分线,∠NAC=60°,
∴∠MAN=120°,
∵∠ABC=∠ADC=90°,
根据四边形的内角和得,∠BCD=360°(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB(角平分线的性质定理),
∴△BCD是等边三角形;
∴∠CDB=60°.
(2)如图②,同(1)得出,∠BCD=60°,

过点C作CE⊥AM于E,CF⊥AN于F,
∵AC是∠MAN的平分线,
∴CE=CF,
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,
在△CDE和△CFB中,
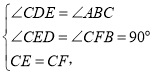
∴△CDE≌△CBF(AAS),
S四边形ABCD![]()
∴四边形ABCD的面积是个定值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级![]() 名学生中抽取
名学生中抽取![]() 名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占
名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占![]() ,明显高于他平时观察到的比例,请回答下列问题:
,明显高于他平时观察到的比例,请回答下列问题:
(1)英语教师所用的调查方式是_______;
(2)如果老师的英语作业检查只得“差”的同学有![]() 名,那么估计全年级的英语作业中可能有多少同学得“差”;
名,那么估计全年级的英语作业中可能有多少同学得“差”;
(3)通过问卷调查,老师得到的数据与事实不符,请你解释这个统计数字失真的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将进货单价40元的商品按50元出售,能卖出500个,已知这种商品每涨价1元,就会少销售10个。为了赚得8000元的利润,售价应定为多少?这时应进货多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时时,另一个点也随之停止运动.设运动时间为t.
(1)用含有t的代数式表示CP.
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设①踢毽子;②篮球;③跳绳;④乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下不完整的两个统计图,依据图中信息,得出下列结论中正确的是( )
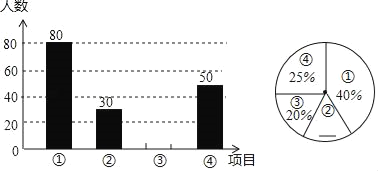
A. 本次共调查300名学生
B. 扇形统计图中,喜欢篮球项目的学生部分所对应的扇形圆心角大小为45°
C. 喜欢跳绳项日的学生人数为60人
D. 喜欢篮球项目的学生人数为30人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】果园要将批水果运往某地,打算租用某汽车运输公司的甲、乙两种货车.以前两次租用这两种货车的信息如表所示:
第一次 | 第二次 | |
甲种货车车辆数(辆) |
|
|
乙种货车车辆数(辆) |
|
|
累计货运量(吨) |
|
|
(1)甲、乙两种货车每辆每次可分别运水果多少吨?
(2)果园现从该汽车运输公司租用甲、乙两种货车共![]() 辆,要求一次运 送这批水果不少于
辆,要求一次运 送这批水果不少于![]() 吨.请你通过计算,求出果园这次至少租用甲种货车多少辆?
吨.请你通过计算,求出果园这次至少租用甲种货车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B坐标为(-2,1).
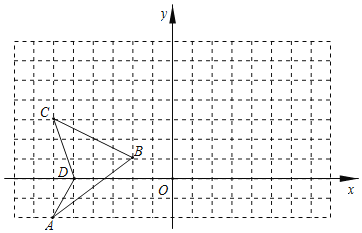
(1)请在图中画出将四边形ABCD关于y轴对称后的四边形A′B′C′D′,并直接写出点A′、B′、C′、D′的坐标;
(2)求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com