Question

如图，在梯形ABCD中，AD∥BC，BC=2AD，点F、G分别是边BC、CD的中点，连接AF、FG，过点D作DE∥FG交AF于点E．
（1）求证：△AED≌△CGF；
（2）若梯形ABCD为直角梯形，∠B=90°，判断四边形DEFG是什么特殊四边形？并证明你的结论；
（3）若梯形ABCD的面积为a（平方单位），则四边形DEFG的面积为______（平方单位）．（只写结果，不必说理）

Answer 1

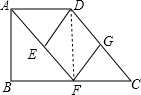
（1）证明：∵BC=2AD，点F为BC的中点，
∴CF=AD．
又∵AD∥BC，
∴四边形AFCD是平行四边形，
∴∠DAE=∠C，AF∥DC，
∴∠AFG=∠CGF．
∵DE∥GF，
∴∠AED=∠AFG，
∴∠AED=∠CGF
∴△AED≌△CGF；

（2）解：结论：四边形DEFG是菱形．
证明如下：连接DF．
由（1）得AF∥DC，
又∵DE∥GF，
∴四边形DEFG是平行四边形．
∵AD∥BC，AD=BF=BC，
∴四边形ABFD是平行四边形，
又∵∠B=90°，
∴四边形ABFD是矩形，
∴∠DFC=90°，
∵点G是CD的中点，
∴FG=DG=CD，
∴四边形DEFG是菱形；

（3）四边形DEFG的面积=梯形ABCD的面积-S_△ABF-2S_△CFG，
∵梯形ABCD的面积为a，
∴四边形DEFG的面积为a；
分析：（1）∵BC=2AD，点F为BC的中点，∴CF=AD．又∵AD∥BC，∴四边形AFCD是平行四边形，∴∠DAE=∠C，AF∥DC，∴∠AFG=∠CGF．∵DE∥GF，∴∠AED=∠AFG，∴∠AED=∠CGF即可证明△AED≌△CGF．
（2）结论：四边形DEFG是菱形，连接DF．由（1）得AF∥DC，又∵DE∥GF，∴四边形DEFG是平行四边形．∵AD∥BC，AD=BF=BC∴四边形ABFD是平行四边形，又∵∠B=90°，∴四边形ABFD是矩形，∴∠DFC=90°．∵点G是CD的中点，∴FG=DG=CD即可证明
四边形DEFG是菱形；
（3）四边形DEFG的面积=梯形ABCD的面积-△ABF-2△CFG即可求解；
点评：本题考查了梯形及全等三角形的判定，难度较大，关键是掌握全等三角形的判定及菱形的判定方法．