
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,CE,BD相交于点O,则图中全等的直角三角形有__对.

【答案】4
【解析】
首先证明△ACE≌△ABD可得AD=AE,EC=BD,根据等式的性质可得AB-AE=AC-AD,即EB=DC;再证明△EBC≌△DCB,△EOB≌△DOC即可.
解:△ACE≌△ABD,△EBC≌△DCB,△EOB≌△DOC,
∵BD、CE为高,
∴∠ADB=∠AEC=,90°,
在△AEC和△ADB中,
∠A=∠A,∠AEC=∠ADB,AB=AC,
∴△ACE≌△ABD(ASA);
∴AD=AE,EC=BD,
∴AB-AE=AC-AD,
即EB=DC,
在△EBC和△DCB中,
EB=DC,BC=BC,EC=DB,∴△EBC≌△DCB(SSS),
在△EOB和△DOC中,
EB=DC,∠OEB=∠ODC,∠EOB=∠DOC,
∴△EOB≌△DOC(AAS).
故答案为:3.
“点睛”本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:
【题目】如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A,B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需再安装一个监控探头,则安装的位置是( )
A.E处
B.F处
C.G处
D.H处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产的一种新型节能灯,为了打开市场出台了相关政策:由厂家协调,厂家按成本价提供产品给经营户自主销售,成本价与出厂价之间的差价由厂家承担.李明按照相关政策投资销售本产品.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始销售的第一个月将销售单价定为20元,那么厂家这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么厂家为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.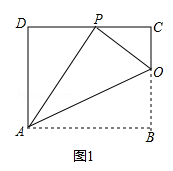
(1)求证:△HCP∽△PDA;
(2)探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
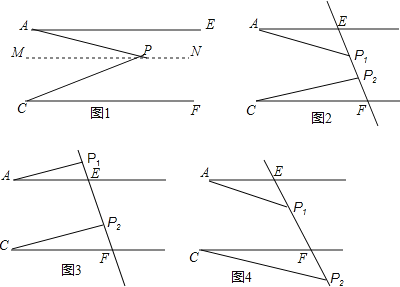
【题目】![]() 已知:如图
已知:如图![]() ,易知
,易知![]() P
P![]() ,请补充完整证明过程:
,请补充完整证明过程:
证明:过点P作![]()
![]() 已作
已作![]()
![]() ______
______![]() ______
______![]() ,
,
又![]()
![]() ______
______![]() ______
______![]()
即![]()
![]() 变式:
变式:
如图![]() 是直线EF上的两点,猜想
是直线EF上的两点,猜想![]()
![]()
![]()
![]() 这四个角之间的关系,并直接写出以下三种情况下这四个角之间的关系.
这四个角之间的关系,并直接写出以下三种情况下这四个角之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com