
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
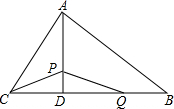 如图,在△ABC中,高AD交边BC于点D,AD=12cm,BD=16cm,CD=8cm.动点P从点D出发,沿折线D-A-B向终点B运动,点P在AD上的速度4cm/s,在AB上的速度5cm/s.同时点Q从点B出发,以6cm/s的速度,沿BC向终点C运动,当点Q停止运动时,点P也随之停止.设点P的运动时间为t(s).
如图,在△ABC中,高AD交边BC于点D,AD=12cm,BD=16cm,CD=8cm.动点P从点D出发,沿折线D-A-B向终点B运动,点P在AD上的速度4cm/s,在AB上的速度5cm/s.同时点Q从点B出发,以6cm/s的速度,沿BC向终点C运动,当点Q停止运动时,点P也随之停止.设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
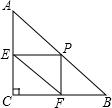 如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.
如图,在△ABC中,∠C=90°,AB=10,$\frac{BC}{AC}$=$\frac{3}{4}$,过AB边上一点P作PE⊥AC于点E,PF⊥BC于点F,则EF的最小值是$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
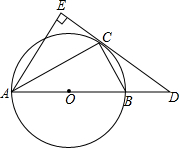 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥DC交DC的延长线于E,AC平分∠DAE.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥DC交DC的延长线于E,AC平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
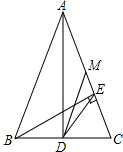 已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
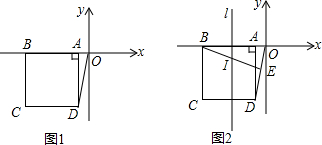
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com