提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案科目：初中数学 来源：2015年初中毕业升学考试（福建莆田卷）数学（解析版） 题型：计算题
（8分）某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数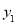
（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数
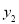（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．
（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（福建莆田卷）数学（解析版） 题型：选择题
（4分）如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（ ）
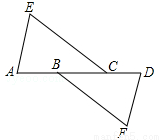
A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江湖州卷）数学（解析版） 题型：解答题
（10分）问题背景：已知在△ABC中，AB边上的动点D由A向B运动（与A，B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连结DE交AC于点F，点H是线段AF上一点
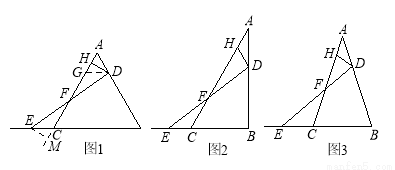
（1）初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，求证：HF=AH+CF
小王同学发现可以由以下两种思路解决此问题：
思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立．
思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立．
请你任选一种思路，完整地书写本小题的证明过程（如用两种方法作答，则以第一种方法评分）
（2）类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是
：1，求
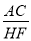的值．
（3）延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记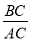
=m，且点D、E的运动速度相等，试用含m的代数式表示 （直接写出结果，不必写解答过程）．
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江湖州卷）数学（解析版） 题型：填空题
在“争创美丽校园，争做文明学生”示范校评比活动中，10位评委给某校的评分情况如下表所示：
评分（分） | 80 | 85 | 90 | 95 |
评委人数 | 1 | 2 | 5 | 2 |
则这10位评委评分的平均数是_________________________分
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江湖州卷）数学（解析版） 题型：选择题
如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
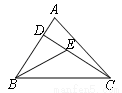
A．10 B．7 C．5 D．4
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（云南昆明卷）数学（解析版） 题型：解答题
（6分）2015年4月25日，尼泊尔发生了里氏8.1级地震，某中学组织了献爱心捐款活动，该校教学兴趣小组对本校学生献爱心捐款额做了一次随机抽样调查，并绘制了不完整的频数分布表和频数分布直方图（每组含前一个边界值，不含后一个边界值）．如图所示：
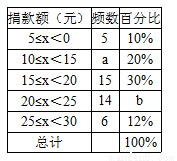
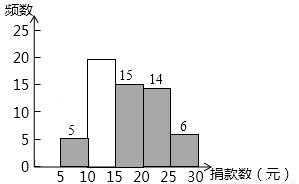
（1）填空：a= ，b= ；
（2）补全频数分布直方图；
（3）该校共有1600名学生，估计这次活动中爱心捐款额不低于20元的学生有多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的次数是 ．