练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若+800元表示盈利800元，那么﹣300元表示（ ）

    A. 收入300元 B. 盈利300元 C. 亏损300元 D. 支出300元

    【答案】C

    【解析】

    “正”和“负”是表示互为相反意义的量，若“盈利”用正数表示，则与它相反意义的量“亏损”用负数表示．

    因为正”和“负”是表示互为相反意义的量,

    所以若“盈利”用正数表示，则与它相反意义的量“亏损”用负数表示，

    所以﹣300元表示亏损300元.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列调查适合抽样调查的是（ ）

    A. 审核书稿中的错别字B. 调查某批汽车的抗撞击能力

    C. 了解八名同学的视力情况D. 企业招聘，对应聘人员进行面试

    查看答案和解析>>

    科目：初中数学 来源： 题型：

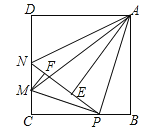
    【题目】如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有 （写出所有正确结论的序号）

    ①△CMP∽△BPA；

    ②四边形AMCB的面积最大值为10；

    ③当P为BC中点时，AE为线段NP的中垂线；

    ④线段AM的最小值为；

    ⑤当△ABP≌△ADN时，BP=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

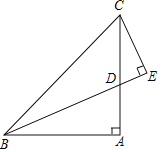
    【题目】如图，在△ABC中，∠BAC=90°，AB=AC，BD平分∠ABC时

    （1）若CE⊥BD于E，①∠ECD=___________0；②求证：BD=2EC；

    （2）如图，点P是射线BA上A点右边一动点，以CP为斜边作等腰直角△CPF，其中∠F＝90°，点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时，点Q是否一定在射线BD上？若在，请证明，若不在；请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若∠α的补角为60°，∠β的余角为60°,则∠α和∠β的大小关系是

    A. ∠α＜∠β B. ∠α＞∠β C. ∠α=∠β D. 无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元。若该商店两次调价的降价率相同，求这个降价率。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与x轴交于A（6，0）、B（，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．

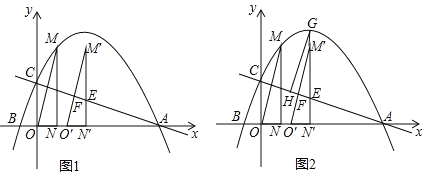
    （1）求此抛物线的解析式；

    （2）如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．

    ①当点F为M′O′的中点时，求t的值；

    ②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设x1，x2是一元二次方程x2﹣2x﹣5＝0的两根，则x12+x22的值为（　　）

    A. 6B. 8C. 14D. 16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△AOB中，∠AOB为直角，OA=6，OB=8，半径为2的动圆圆心Q从点O出发，沿着OA方向以1个单位长度/秒的速度匀速运动，同时动点P从点A出发，沿着AB方向也以1个单位长度/秒的速度匀速运动，设运动时间为t秒（0＜t≤5）以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连结CD、QC．

    （1）当t为何值时，点Q与点D重合？

    （2）当⊙Q经过点A时，求⊙P被OB截得的弦长．

    （3）若⊙P与线段QC只有一个公共点，求t的取值范围．

    查看答案和解析>>

    同步练习册答案