
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(﹣3,0),点B坐标为(1,0),点C在y轴的正半轴,且∠CAB=30°.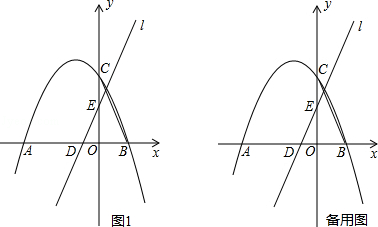
(1)求抛物线的函数解析式;
(2)若直线l:y= ![]() x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
①当m>0时,在线段AC上否存在点P,使得点P,D,E构成等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
②以动直线l为对称轴,线段AC关于直线l的对称线段A′C′与二次函数图象有交点,请直接写出m的取值范围.
【答案】
(1)
解:如图1,连结AC,在Rt△AOC中,∠CAB=30°,
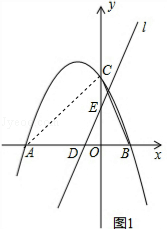
∵A(﹣3,0),即OA=3,
∴OC= ![]() ,即C(0,
,即C(0, ![]() ),
),
设抛物线解析式为 ![]() ,
,
将A(﹣3,0),B(1,0)代入得 ![]() .
.
解得 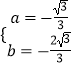 .
.
∴ ![]()
(2)
解:由题意可知,OE=m,OD= ![]() ,∠DEO=30°,
,∠DEO=30°,
(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴
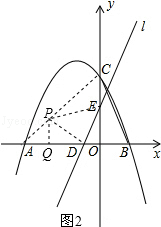
∴∠PQD=∠EOD=90°,
∠PDQ+∠EDO=90°,∠EDO+∠DEO=90°,
∴∠DEO=∠PDQ=30°,
在△DPQ与△EDO中,
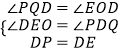 ,
,
∴△DPQ≌△EDO(AAS),
∴DQ=OE=m,
∵∠PAQ=∠PDQ=30°,
∴PA=PD,
∴AQ=DQ=m,
∴OA=2m+ ![]() =3,
=3,
∴ ![]() ;
;
(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴,
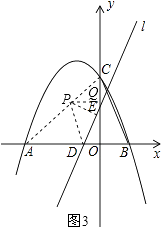
同理可得CQ=EQ=OD= ![]() ,
,
∴OC=m+ ![]() =
= ![]() ,
,
∴ ![]() ;
;
(iii)如图4,当DP⊥PE,DP=PE,作DM⊥AC,EN⊥AC,
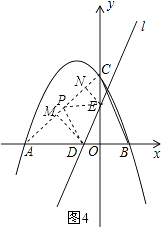
同理可得AP=AD= ![]() ,PN=DM=
,PN=DM= ![]() ,CN=
,CN= ![]()
∴AC= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() ;
;
②当x=0,y= ![]() 时,
时, ![]() =0+m,解得m=
=0+m,解得m= ![]() ;
;
当x=0,y=﹣ ![]() 时,﹣
时,﹣ ![]() =0+m,解得m=﹣
=0+m,解得m=﹣ ![]() .
.
故m的取值范围为: ![]()
【解析】(1)如图1,连结AC,在Rt△AOC中,∠CAB=30°,根据三角函数可得C(0, ![]() ),根据待定系数法可求抛物线解析式;(2)①由题意可知,OE=m,OD=
),根据待定系数法可求抛物线解析式;(2)①由题意可知,OE=m,OD= ![]() ,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴;(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴;(iii)如图4,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC;进行讨论可求点P的坐标;②动直线l与直线AC的交点为C和动直线l与y轴的交点在x轴下面,并且与前面的直线平行,可求m的取值范围.
,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴;(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴;(iii)如图4,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC;进行讨论可求点P的坐标;②动直线l与直线AC的交点为C和动直线l与y轴的交点在x轴下面,并且与前面的直线平行,可求m的取值范围.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如题![]() ,
,![]() ,点
,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的一个动点,作
上的一个动点,作![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() .
.
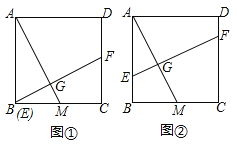
(1)如图①,当点![]() 于点
于点![]() 重合时,求证:
重合时,求证:![]() ;
;
(2)设![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数解析式,并写出定义域.
的函数解析式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按以下规律排列:

表中数2在第二行第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应,根据这一规律,数2014对应的有序数对为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a=__,![]() =____;
=____;
(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(0,4).
(1)求此一次函数的解析式;
(2)当y=-5时求x的值;
(3)求此函数图象与两坐标轴所围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间休息时小明拿着两根木棒玩,小华看到后要小明给他玩,小明说:“较短木棒AB长40cm,较长木棒CD长60cm,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E和点F,则点E和点F间的距离是多少?你说对了我就给你玩”聪明的你请帮小华求出此时两根木棒的中点E和F间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)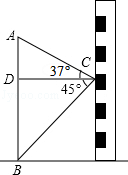
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,点O为AD中点,点E在BD上,连接EO并延长交BC于点F,连接BE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=3![]() ,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 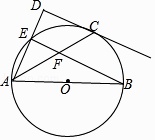
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com