【题目】如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是（ ）
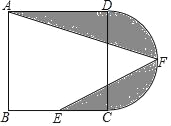
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
【答案】C
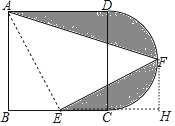
【解析】作FH⊥BC于H，连接FH，如图，根据正方形的性质和切线的性质得BE=CE=CH=FH=6，则利用勾股定理可计算出AE=6
，通过Rt△ABE≌△EHF得∠AEF=90°，然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算．
作FH⊥BC于H，连接FH，如图，
∵点E为BC的中点，点F为半圆的中点，
∴BE=CE=CH=FH=6，
AE=
=6，
易得Rt△ABE≌△EHF，
∴∠AEB=∠EFH，
而∠EFH+∠FEH=90°，
∴∠AEB+∠FEH=90°，
∴∠AEF=90°，
∴图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF
=12×12+
π62﹣×12×6﹣6×6
=18+18π．
故选：C．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图A村和B村在一条大河CD的同侧，它们到河岸的距离AC、BD分别为1千米和4千米，又知道CD的长为4千米.
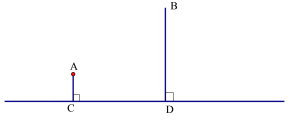
（1）现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
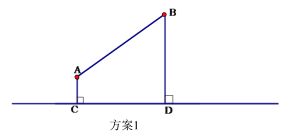
方案1：水厂建在C点，修自来水管道到A村，再到B 村（即AC+AB）.（如图）
方案2：作A点关于直线CD的对称点
，连接
交CD 于M点，水厂建在M点处，分别向两村修管道AM和BM. （即AM+BM） （如图）
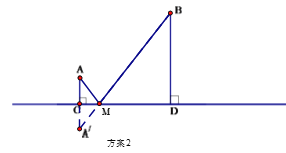
从节约建设资金方面考虑，将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算，判断哪种方案更合适.
（2）有一艘快艇Q从这条河中驶过，当快艇Q与CD中点G相距多远时，△ABQ为等腰三角形？直接写出答案，不要说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市用
元购进某种干果销售，由于销售状况良好，超市又调拨
元资金购进该种干果，但这次的进价比第一次的进价提高了
，购进干果数量是第一次的
倍还多
千克．
该种干果的第一次进价是每千克多少元？
如果超市将这种干果全部按每千克
元的价格出售，售完这种干果共盈利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
为线段
上一动点(不与点
，
重合)，在同侧分别作等边
和等边
，
与
交于点
，与
交于点
，与
交于点
，连接
.下列五个结论：①
；②
；③
；④DE=DP；⑤
.其中正确结论的个数是( )
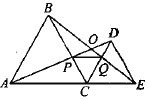
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠A=30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD=2
，则线段CD的长是（ ）
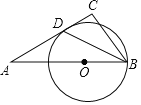
A. 2 B. C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了
箭,他们的总成绩(单位:环)相同．小宇根据他们的成绩绘制了如图尚不完整的统计图表，并计算了甲成绩的平均数和方差(见小宇的作业)．
第 | 第 | 第 | 第 | 第 | |
甲成绩 |
|
|
|
|
|
乙成绩 |
|
|
|
|
|
（1）a=_________
（2）
（3）参照小宇的计算方法，计算乙成绩的方差；
（4）请你从平均数和方差的角度分析，谁将被选中．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A、B在反比例函数y=
的图象上，过点A、B作x轴的垂线，垂足分别是M、N，射线AB交x轴于点C，若OM=MN=NC，四边形AMNB的面积是3，则k的值为（ ）
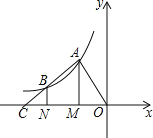
A．2 B．4 C．﹣2 D．﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一块形如四边形ABCD的草地中，AB＝3m，BC＝4m，CD＝12m，DA＝13m，且∠ABC＝90°，要以AC、CD、DA为边制作围栏，问围栏长多少米，草地面积多大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
