
【题目】如图A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
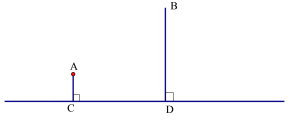
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
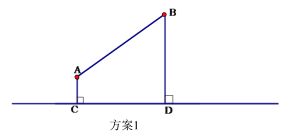
方案1:水厂建在C点,修自来水管道到A村,再到B 村(即AC+AB).(如图)
方案2:作A点关于直线CD的对称点![]() ,连接
,连接![]() 交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
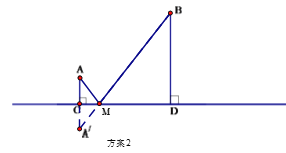
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q与CD中点G相距多远时,△ABQ为等腰三角形?直接写出答案,不要说明理由.
【答案】(1)方案1更合适;(2)QG=![]() 时,△ABQ为等腰三角形.
时,△ABQ为等腰三角形.
【解析】
(1)分别求出两种路线的长度进行比较;(2)分类讨论,然后解直角三角形.

(1)过A点作AE⊥BD于E,
∵BD=4,AC=1,
∴BE=3.
∵AE=CD=4,BE=3,
在△ABE中,根据勾股定理得:
AB=![]() ,
,
=5.

过A,作A,H⊥BD于H,
在直角三角形A,HB中,根据勾股定理得:
A,B=![]() ,
,
=![]() ,
,
=![]() ,
,
方案①AC+AB=1+5=6.
方案②AM+MB=A,B=![]() .
.
∵6<![]() ,
,
∴方案①路线短,比较合适.
(2)

过A点以AB为半径作圆交CD于E和F点,
图中由勾股定理求得EC=CF=2![]() .所以QG=2
.所以QG=2![]() -2或2
-2或2![]() +2.
+2.

过B点为圆心以AB为半径作圆,交CD于G、H.
由勾股定理可求得:GD=DH=3,所以QG=1或5.

做AB的垂直平分线交CD于Q,
求得:QG=![]() .
.
综上, QG=![]() 时,△ABQ为等腰三角形.
时,△ABQ为等腰三角形.


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
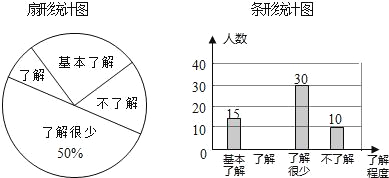
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 都为等腰直角三角形,
都为等腰直角三角形,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() .
.

(1)若![]() ,求
,求![]() 的周长;
的周长;
(2)如图![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).①如图1,若BC=4m,则S= m2.②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变则在BC的变化过程中,当S取得最小值时,边BC的长为 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
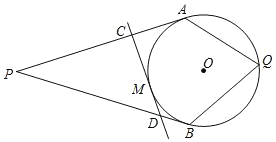
【题目】如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).
(1)若PA=10,求△PCD的周长;
(2)若∠P=40°,求∠AQB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
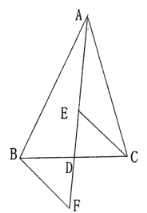
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 延长线上的点,且
延长线上的点,且![]() ,连接
,连接![]() 、
、![]() ,下列说法:①
,下列说法:①![]() 和
和![]() 的面积相等,②
的面积相等,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中一定正确的答案有______________.(只填写正确的序号)
,其中一定正确的答案有______________.(只填写正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
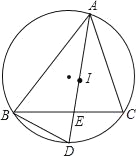
【题目】如图,点I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,与BC相交于点E.
(1)求证:DI=DB;
(2)若AE=6cm,ED=4cm,求线段DI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
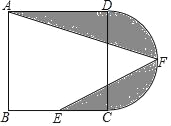
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com