
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).①如图1,若BC=4m,则S= m2.②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变则在BC的变化过程中,当S取得最小值时,边BC的长为 m.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
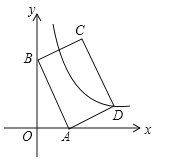
【题目】如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数![]() (x>0)的图像经过点D,则
(x>0)的图像经过点D,则![]() 值为( )
值为( )
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°

(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
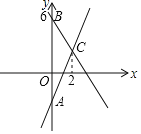
【题目】如图,一次函数y1=2x﹣2的图象与y轴交于点A,一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象交点,且点C的横坐标为2.
(1)求一次函数y2的函数解析式;
(2)求△ABC的面积;
(3)问:在坐标轴上,是否存在一点P,使得S△ACP=2S△ABC,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
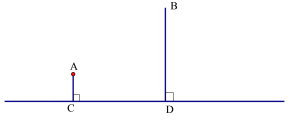
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
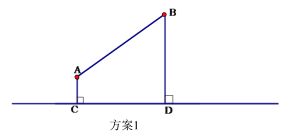
方案1:水厂建在C点,修自来水管道到A村,再到B 村(即AC+AB).(如图)
方案2:作A点关于直线CD的对称点![]() ,连接
,连接![]() 交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
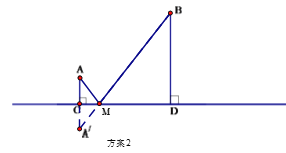
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q与CD中点G相距多远时,△ABQ为等腰三角形?直接写出答案,不要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .设
.设![]() 为最长边.当
为最长边.当![]() 时,
时,![]() 是直角三角形;当
是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,探究
的大小关系,探究![]() 的形状(按角分类).
的形状(按角分类).
(1)当![]() 三边分别为6、8、9时,
三边分别为6、8、9时,![]() 为______三角形;当
为______三角形;当![]() 三边分别为6、8、11时,
三边分别为6、8、11时,![]() 为______三角形.
为______三角形.
(2)猜想,当![]() ______
______![]() 时,
时,![]() 为锐角三角形;当
为锐角三角形;当![]() ______
______![]() 时,
时,![]() 为钝角三角形.
为钝角三角形.
(3)判断当![]() ,
,![]() 时,
时,![]() 的形状,并求出对应的
的形状,并求出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
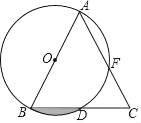
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
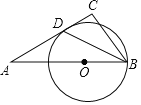
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com