
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°

(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
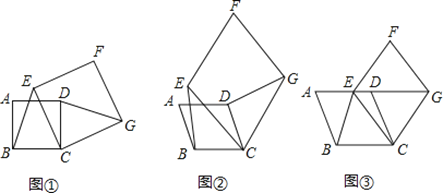
【题目】感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.
探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
应用:如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED, ∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
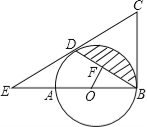
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
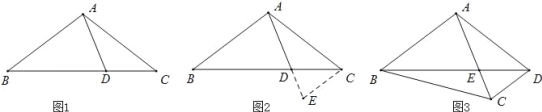
【题目】阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).①如图1,若BC=4m,则S= m2.②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变则在BC的变化过程中,当S取得最小值时,边BC的长为 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com