
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
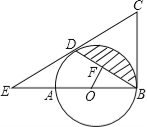
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
【答案】解:(1)证明:连接OD,
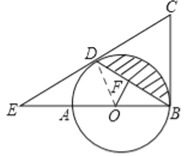
∵BC是⊙O的切线,∴∠ABC=90°。
∵CD=CB,∴∠CBD=∠CDB。
∵OB=OD,∴∠OBD=∠ODB。
∴∠ODC=∠ABC=90°,即OD⊥CD。
∵点D在⊙O上,∴CD为⊙O的切线。
(2)在Rt△OBF中,∵∠ABD=30°,OF=1,∴∠BOF=60°,OB=2,BF=![]() 。
。
∵OF⊥BD,∴BD=2BF=2![]() ,∠BOD=2∠BOF=120°,
,∠BOD=2∠BOF=120°,
∴![]() 。
。
【解析】(1)连接OD,由BC是⊙O的切线,可得∠ABC=90°,由CD=CB,OB=OD,易证得∠ODC=∠ABC=90°,即可证得CD为⊙O的切线。
(2)在Rt△OBF中,∠ABD=30°,OF=1,可求得BD的长,∠BOD的度数,又由![]() ,即可求得答案。
,即可求得答案。


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:第19届亚洲运动会将于2022年9月10日至25日在杭州举行,杭州奥体博览城将成为杭州2022年亚运会的主场馆,某工厂承包了主场馆建设中某一零件的生产任务,需要在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多![]() ,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
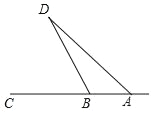
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
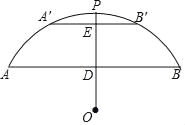
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米,
(1)求圆弧所在的圆的半径r的长;
(2)若拱顶离水面只有4米,即PE=4米时,求它的跨度A′B′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款机器人进行销售,很快销售一空,商家又用
元购进某款机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款机器人,所购进数量是第一次的
元第二次购进同款机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() 不考虑其他因素
不考虑其他因素![]() ,那么每个机器人的标价至少是多少元?
,那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°

(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com