【题目】如图，
中，
，且
，则
________．
【答案】
【解析】
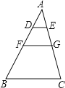
由DE∥FG∥BC，平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，即可判定△ADE∽△AFG∽△ABC，根据相似三角形的面积比等于相似比的平方，即可求得
，
，设S△ADE=4x，即可求得S梯形DFGE与S梯形FBCG的值，继而求得S△ADE：S梯形DFGE：S梯形FBCG的值．
∵△ABC中，DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∴
，
∵AD：DF：FB=2：3：4，
∴
，
，
∴，，
设S△ADE=4x，则S△AFG=25x，S△ABC=81x，
∴S梯形DFGE=25x-4x=21x，S梯形FBCG=81x-25x=56x，
∴S△ADE：S梯形DFGE：S梯形FBCG=4：21：56．
故答案为：4：21：56．
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
【题目】八年级（1）班从学校出发去某景点旅游，全班分成甲、乙两组，甲组乘坐大型客车，乙组乘坐小型客车．已知甲组比乙组先出发，汽车行驶的路程
(单位:
)和行驶时间
(单位:
)之间的函数关系如图所示．
根据图象信息，回答下列问题：
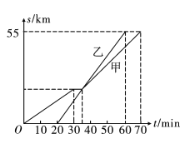
（1）学校到景点的路程为_ ，甲组比乙组先出发 ， 组先到达旅游景点；
（2）求乙组乘坐的小型客车的平均速度；
（3）从图象中你还能获得哪些信息？ (请写出一条)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD=CB，延长CD交BA的延长线于点E．
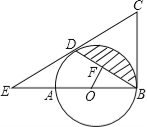
（1）求证：CD为⊙O的切线；
（2）若BD的弦心距OF=1，∠ABD=30°，求图中阴影部分的面积．（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是( )
A. 各有一个角是
的两个等腰三角形相似 B. 各有一个角是
的两个等腰三角形相似
C. 有两边对应成比例的两个等腰三角形相似 D. 两腰对应成比例的两个等腰三角形相似
查看答案和解析>>
科目：初中数学 来源： 题型：
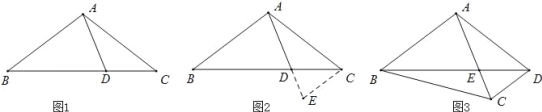
【题目】阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的长．
小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图 2）．
请回答：∠ACE的度数为 ，AC的长为 ．
参考小腾思考问题的方法，解决问题：
如图 3，在四边形 ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2ED，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在边长为1的小正方形网格中，△AOB的顶点均在格点上．
（1）B点关于y轴的对称点坐标为 ；
（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；
（3）在（2）的条件下，A1的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
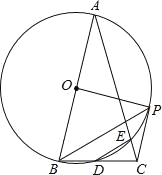
【题目】如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，连结DE，过点B作BP平行于DE，交⊙O于点P，连结EP、CP、OP．
（1）BD=DC吗？说明理由；
（2）求∠BOP的度数；
（3）求证：CP是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
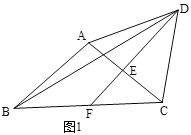
【题目】在△ABC中，AB=AC，在△ABC的外部作等边三角形△ACD，E为AC的中点，连接DE并延长交BC于点F，连接BD．
（1）如图1，若∠BAC=100°，则∠ABD的度数为_____，∠BDF的度数为______；
（2）如图2，∠ACB的平分线交AB于点M，交EF于点N，连接BN，若BN=DN，∠ACB=
．
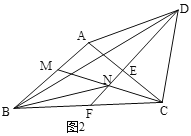
(I)用表示∠BAD；
(II)①求证：∠ABN=30°；
②直接写出的度数以及△BMN的形状．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
