
【题目】在等边![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
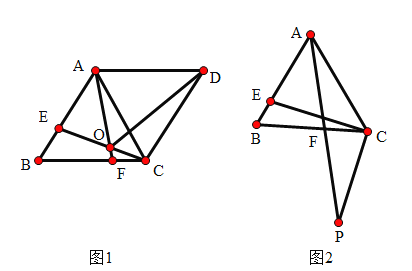
(1)如图![]() ,若
,若![]() ,以
,以![]() 为边作等边
为边作等边![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
求证:①![]() ;
;
②![]() 平分
平分![]() .
.
(2)如图![]() ,若
,若![]() ,作
,作![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .
.
【答案】(1)①见解析;②见解析;(2)见解析
【解析】
(1)①利用SAS即可证出△ABF≌△CAE,再根据全等三角形的性质即可证出结论;
②过点D作DM⊥AF于M,作DN⊥EC交EC延长线于N,利用AAS证出△ADM≌△CDN,即可得出DM=DN,然后根据角平分线的判定定理即可证出结论;
(2)在CB上截取一点G,使CF=FG,连接AG,利用SAS证出△EAC≌△GCA,可得CE=AG,∠AEC=∠CGA,然后利用ASA证出△AGF≌△PCF,可得AG=CP,从而证出结论.
解:(1)①△ABC为等边三角形
∴AB=CA,∠B=∠CAE=∠BAC=60°
在△ABF和△CAE中
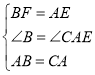
∴△ABF≌△CAE
∴![]()
②过点D作DM⊥AF于M,作DN⊥EC交EC延长线于N
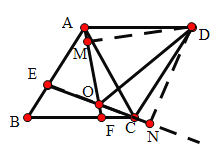
∵△ABF≌△CAE
∴∠BAF=∠ACE
∴∠AOC=180°-∠ACE-∠OAC=180°-∠BAF-∠OAC=180°-∠BAC=120°
∴∠MDN=360°-∠AOC-∠DMO-∠DNO=60°
∵△ACD为等边三角形
∴DA=DC,∠ADC=60°
∴∠ADC=∠MDN
∴∠ADC-∠MDC=∠MDN-∠MDC
∴∠ADM=∠CDN
在△ADM和△CDN中
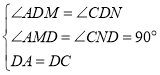
∴△ADM≌△CDN
∴DM=DN
∴![]() 平分
平分![]()
(2)在CB上截取一点G,使CF=FG,连接AG
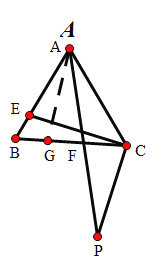
∵AE=2CF,CG=CF+FG=2CF
∴AE=CG
∵△ABC为等边三角形
∴∠EAC=∠GCA=60°
在△EAC和△GCA中
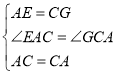
∴△EAC≌△GCA
∴CE=AG,∠AEC=∠CGA
∵∠AEC=∠BCP
∴∠CGA=∠BCP,即∠AGF=∠PCF
在△AGF和△PCF中
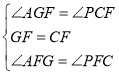
∴△AGF≌△PCF
∴AG=CP
∴CE=CP


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
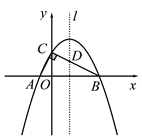
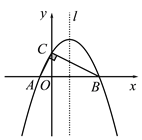
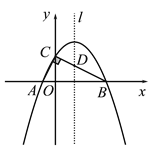
图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
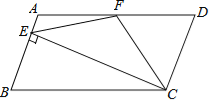
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:第19届亚洲运动会将于2022年9月10日至25日在杭州举行,杭州奥体博览城将成为杭州2022年亚运会的主场馆,某工厂承包了主场馆建设中某一零件的生产任务,需要在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多![]() ,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BC=2,E、F分别为射线BC,CD上两个动点,且满足BE=CF,设AE,BF交于点G,连接DG,则DG的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形.点C也在格点上,且△ABC为等腰三角形,则符合条件的点C有( )个.
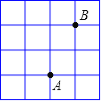
A.3B.5C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
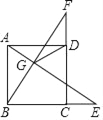
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 .
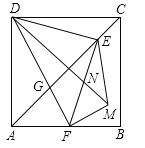
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
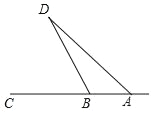
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com