
����Ŀ����ͼ����Rt��ABC�Ķ���A��B��x���ϣ���C��y�����������ϣ���
A(��1��0)��B(4��0)����ACB��90��.
(1)���A��B��C����������߽���ʽ��
(2)�������ߵĶԳ���l��BC�߽��ڵ�D����P�ǶԳ���l�ϵĵ㣬��������P��C��DΪ��������������AOC���ƣ���P������ꣻ
(3)�ڶԳ���l�����������Ƿ�ֱ���ڵ�M��N��ʹ����A��O��M��NΪ������ı�����ƽ���ı��Σ���������ֱ��д����M����N�����ꣻ�������ڣ���˵������.
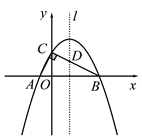
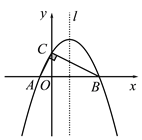
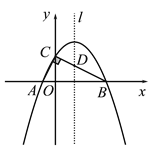
ͼ1 ����ͼ
���𰸡�������
��������������(1)����![]() �����
�����![]() �����꣬�ô���ϵ����������������ߵĽ���ʽ.
�����꣬�ô���ϵ����������������ߵĽ���ʽ.
(2)����������������ۼ���.
(3)����. ����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.�ֵ�ƽ���ı���![]() ��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��⣺(1)��֤![]() ����
����![]() ��
��![]()
��OC=2����C(0��2),
�������߹���A(-1��0)��B(4��0)
��˿��������ߵĽ���ʽΪ![]()
��C��(0��2)�����:![]() ����
����![]()
�������ߵĽ���ʽΪ![]()
(2)��ͼ2��
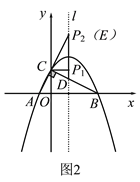
��![]() ʱ��
ʱ��![]() ��P1(
��P1(![]() ��2),
��2),
��![]() ʱ��
ʱ��![]()
��OC��l,
��![]() ��
��
��P2H��![]() ��OC��5��
��OC��5��
��P2 (![]() ��5)
��5)
���P�������Ϊ(![]() ��2)��(
��2)��(![]() ��5).
��5).
(3)����.
����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.
��ͼ3��
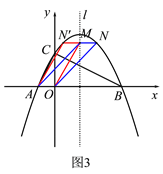
��ƽ���ı���![]() ��ƽ���ı���ʱ��M(
��ƽ���ı���ʱ��M(![]() ��
��![]() )��
)��![]() (
(![]() ,
,![]() ),
),
��ƽ���ı���AONM��ƽ���ı���ʱ��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ),
),
��ͼ4�����ı���AMONΪƽ���ı���ʱ��MN��OA����ƽ�֣���ʱ����M(![]() ��m)����
��m)���� ![]()

����N��������![]() �ϣ�
�ϣ�
��-m��-![]() ��(-
��(-![]() +1)( -
+1)( -![]() -4)=-
-4)=-![]() ,
,
��m=![]() ,
,
��ʱM(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).
����������M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() )��M(
)��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ) �� M(
) �� M(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ,
, ![]() ����
����![]() .
.
(1)���߶� ![]() �ij�;
�ij�;
(2)���� ![]() �ӵ�
�ӵ� ![]() ���������߶�
���������߶� ![]() ��ÿ�� 1 ����λ���ȵ��ٶ����յ�
��ÿ�� 1 ����λ���ȵ��ٶ����յ� ![]() �˶�������
�˶������� ![]() �� ��
�� �� ![]() ����������
����������![]() ��ÿ�� 4 ����λ���ȵ��ٶ��˶���
��ÿ�� 4 ����λ���ȵ��ٶ��˶���![]() ����ͬʱ����������
����ͬʱ���������� ![]() ����
���� ![]() ��ʱ��
��ʱ��![]() ����ͬʱֹͣ�˶�.���
����ͬʱֹͣ�˶�.��� ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ ![]() �룬
�룬![]() �����Ϊ
�����Ϊ ![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ ![]() ����ֱ��д����Ӧ��
����ֱ��д����Ӧ�� ![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
(3)��(2)�������£��� ![]() ��ֱ��
��ֱ��![]() �ϵ�һ����
�ϵ�һ���� ![]() .�Ƿ����
.�Ƿ����![]() ֵ��ʹ�Ե�
ֵ��ʹ�Ե� ![]() Ϊ�� ������������Ե�
Ϊ�� ������������Ե� ![]() Ϊ�����������ȫ��?�����ڣ���ֱ��д������������
Ϊ�����������ȫ��?�����ڣ���ֱ��д������������ ![]() ֵ; �������ڣ���˵������.
ֵ; �������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
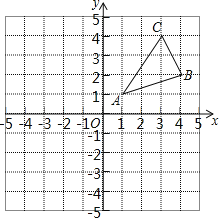
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У���ABC�������������ֱ���A(1��1)��B (4��2)��C(3��4)��
��1��������ABC����y��ԳƵ���A1B1C1��Ҫ��A��A1��B��B1��C��C1���Ӧ����
��2��ͨ����ͼ����x����ȷ����Q��ʹ��QA��QB֮����С������QA��QB����ֱ��д����Q�����꣮��Q������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����ؼƻ�װ�˼ס��ҡ�������ˮ����������ۣ�ÿ�������涨���أ�����ֻװһ��ˮ���������Ϊװ�˼ס��ҡ�������ˮ��������������
�� | �� | �� | |
ÿ��������װ���������֣� | 4 | 2 | 3 |
ÿ��ˮ���ɻ�����ǧԪ�� | 5 | 7 | 4 |
��1����8������װ���ҡ�������ˮ����22�ֵ�A�����ۣ���װ���ҡ�������ˮ������������������
��2��ˮ�����ؼƻ���20������װ�˼ס��ҡ�������ˮ����72�ֵ�B��������ÿ��ˮ��������һ����������װ�˼�ˮ��������Ϊm������װ���ҡ�������ˮ�������������������������m��ʾ��
��3���ڣ�2���ʵĻ����ϣ���ΰ���װ�˿�ʹˮ�����ػ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ����ϲ����һ�������Ŀ�������ȫУ����ѧ��������һ�ε��ˣ����˽�������������A����ѧ������B���Ƽ�������C�������˶����������������Ƴ����µIJ�����ͳ��ͼ��
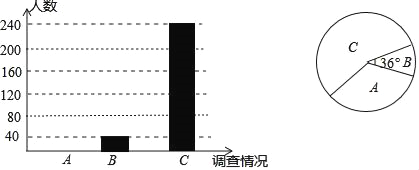
����������Ϣ������������⣺
��1�����λ�������˶�����ѧ����
��2��������ͳ��ͼ�������������������ͳ��ͼ��A�������ε�Բ�ĽǵĶ�����
��3������У����1400��ѧ�����Թ��Ƹ�Уѧ������ϲ����ѧ�����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����������ҹ���������ѧ�����������������е�һ�����⣬������Բ�ģ����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ��� ���ִ�����ѧ���Ա����ǣ�����ͼ��CD�ǡ�O��ֱ������AB��CD������ΪE��CE = 1�磬AB = 1�ߣ���ֱ���ij���. �����⣬CD��Ϊ�� ��
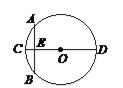
A. ![]() �� B. 13�� C. 25�� D. 26��
�� B. 13�� C. 25�� D. 26��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ�![]() �У���
����![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ���ӳ����ϣ�
���ӳ����ϣ�![]() ����ͼ1��
����ͼ1��
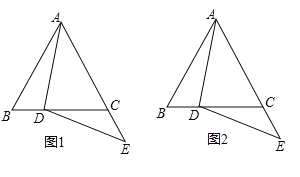
��1����֤��![]() ��
��
��2����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ��
��![]() ��
��
�������⽫ͼ2��ȫ��
��֤�����ڵ�![]() �˶��Ĺ����У�ʼ����
�˶��Ĺ����У�ʼ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
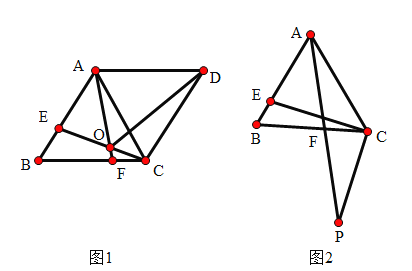
����Ŀ���ڵȱ�![]() �У���
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�
��1����ͼ![]() ����
����![]() ����
����![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
��֤����![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
��2����ͼ![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com