
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
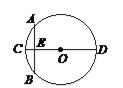
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图.

(1)根据图象,求油箱中的余油Q与行驶时间t的函数关系式;
(2)从外出开始算起,如果汽车每小时行驶50千米.当油箱中余油30升时,该汽车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,并连结CN.求证:AB=CN+CM.
(2)(类比探究)如图2,在等边△ABC中,若点M是BC延长线上的任意一点(不含端点C),其它条件不变,则AB=CN+CM是否还成立?若成立,请说明理由;若不成立,请写出AB,CN,CM三者之间的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,AB=10![]() ,点G为AC中点,连接BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH,以下结论:①∠ACE=∠ABG;②CF=
,点G为AC中点,连接BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH,以下结论:①∠ACE=∠ABG;②CF=![]() ;③∠AGE=∠CGB;④FH平分∠BFE,其中正确的结论有( )个.
;③∠AGE=∠CGB;④FH平分∠BFE,其中正确的结论有( )个.
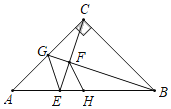
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西,简称“陕”或“秦”,古老而神秘,犹如镶嵌在中国内陆腹地的一颗明珠,是中华民族的重要发祥地之一,也是烹饪文化的重要发源地.陕西著名的特色美食中,馍类有:炕炕馍、石子馍(分别记为A1、A2);糕点类有:水晶饼、琼锅糖(分别记为B1、B2);面食类有:臊子面、荞面饸饹(分别记为C1、C2).肖晓和陈梅同时去品尝陕西美食,肖晓打算在炕炕馍、水晶饼、荞面饸饹这三种美食中选择一种,陈梅打算在石子馍、琼锅糖、臊子面这三种美食中选择一种.
(1)用画树状图或列表法表示肖晓和陈梅选择美食的所有可能结果;
(2)求肖晓和陈梅同时选择的美食不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
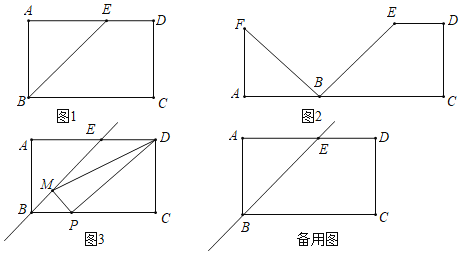
【题目】如1,在矩形ABCD中,AB=6,AD=10,E为AD上一点且AE=6,连接BE.
(1)将△ABE绕点B逆时针旋转90°至△ABF(如图2),且A、B、C三点共线,再将△ABF沿射线BC方向平移,平移速度为每秒1个单位长度,平移时间为t(s)(t≥0),当点A与点C重合时运动停止.
①在平移过程中,当点F与点E重合时,t= (s).
②在平移过程中,△ABF与四边形BCDE重叠部分面积记为S,求s与t的关系式.
(2)如图3,点M为直线BE上一点,直线BC上有一个动点P,连接DM、PM、DP,且EM=5![]() ,试问:是否存在点P,使得△DMP为等腰三角形?若存在,请直接写出此时线段BP的长;若不存在,请说明理由.
,试问:是否存在点P,使得△DMP为等腰三角形?若存在,请直接写出此时线段BP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
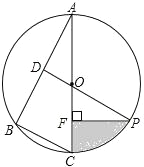
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com