
【题目】如图,△ABC中,∠ACB=90°,AC=BC,AB=10![]() ,点G为AC中点,连接BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH,以下结论:①∠ACE=∠ABG;②CF=
,点G为AC中点,连接BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH,以下结论:①∠ACE=∠ABG;②CF=![]() ;③∠AGE=∠CGB;④FH平分∠BFE,其中正确的结论有( )个.
;③∠AGE=∠CGB;④FH平分∠BFE,其中正确的结论有( )个.
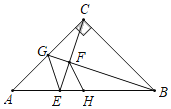
A.1B.2C.3D.4
【答案】B
【解析】
如图,作AP⊥AC交CE的延长线于P,连接CH.构造全等三角形,证明△CAP≌△BCG(ASA),△EAG≌△EAP(SAS),即可判断(3)正确,利用四点共圆可以证明(4)正确,解直角三角形可以判定(2)错误.
解:如图,作AP⊥AC交CE的延长线于P,连接CH.
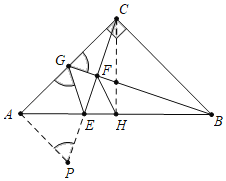
∵CE⊥BG,
∴∠CFB=∠ACB=90°,
∵∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,
∴∠ACE=∠CBG,
∵BG是△ABC的中线,AB>BC,
∴∠ABG≠∠CBG,
∴∠ACE≠∠ABG,故(1)不合题意,
∵∠ACP=∠CBG,AC=BC,∠CAP=∠BCG=90°,
∴△CAP≌△BCG(ASA),
∴CG=PA=AG,∠BGC=∠P,
∵AG=AP,∠EAG=∠EAP=45°,AE=AE,
∴△EAG≌△EAP(SAS),
∴∠AGE=∠P,
∴∠AGE=∠CGB,故(3)符合题意,
∵AB=10![]() ,△ABC是等腰直角三角形,
,△ABC是等腰直角三角形,
∴AC=BC=10,
∴AG=CG=5,
∴BG=![]() =5
=5![]() ,
,
∵![]() CGCB=
CGCB=![]() BGCF,
BGCF,
∴CF=2![]() ,故(2)不合题意,
,故(2)不合题意,
∵CA=CB,∠ACB=90°,AH=HB,
∴∠BCH=∠ACH=45°,
∵∠CFB=∠CHB=90°,
∴C,F,H,B四点共圆,
∴∠HFB=∠BCH=45°,
∴∠EFH=∠HFB=45°,
∴FH平分∠BFE,故(4)符合题意,
故选:B.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲.乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①100秒时乙到达终点;②a=8;③b=92④c=125,其中正确的是( )

A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
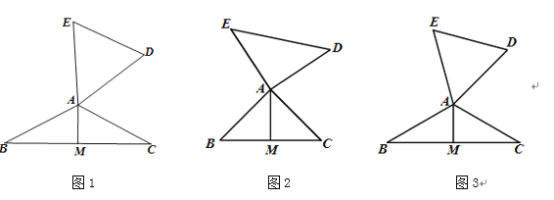
(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。
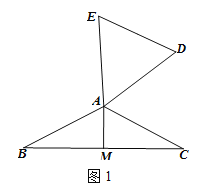
(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。
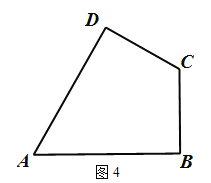
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
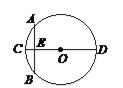
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,鲁能巴蜀中学团委决定组织同学们观看电影《我和我的祖国》,《中国机长》和《攀登者》,小明准备到电影院提前购票.已知三部电影单价之和为100元,计划购买三部电影票总共不超过135张;其中《攀登者》票价为30元,计划购买35张,《中国机长》至少购买25张,《我和我的祖国》数量不少于《中国机长》的2倍粗心的小明在做预算时将《我和我的祖国》和《中国机长》的票价弄反了,结果实际购买三种电影票时的总价比预算多了112元,若三部电影票的单价均为整数,则小明实际购买这三部电影票最多需要花费_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校对初2021级甲、乙两班各60名学生进行知识测试(满分60分),测试完成后分别抽取了12份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班12名学生测试成绩统计如下:
45,59,60,38,57,53,52,58,60,50,43,49
乙班12名学生测试成绩统计如下:
35,55,46,39,54,47,43,57,42,59,60,47
(整理数据)
按如下分数段整理,描述这两组样本数据
组别频数 |
|
|
|
|
|
甲 | 0 | 1 | 3 | 3 | 5 |
乙 | 2 | 2 | 3 | 1 | 4 |
(分析数据)
两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 |
甲 |
| 52.5 | |
乙 | 48.7 | 47 |
|
(1)![]() ,
,![]() ;
;
(2)若规定得分在40分及以上为合格,请估计乙班60名学生中知识测试合格的学生有多少人?
(3)你认为哪个班的学生知识测试的整体水平较好,请说明一条理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°.
(1)用直尺和圆规作⊙O,使它经过A、B、D三点(保留作图痕迹);
(2)点C是否在⊙O上?请说明理由.
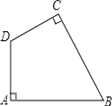
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com