
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
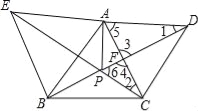
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

【答案】(1)证明见解析(2)证明见解析
【解析】
试题分析:(1)①根据题意,利用内角和定理及等式性质得到一对角相等,利用两角相等的三角形相似即可得证;
②由三角形ABP与三角形BCP相似,得比例,将PA与PC的长代入求出PB的长即可;
(2)①根据三角形ABE与三角形ACD为等边三角形,利用等边三角形的性质得到两对边相等,两个角为60°,利用等式的性质得到夹角相等,利用SAS得到三角形ACE与三角形ABD全等,利用全等三角形的对应角相等得到∠1=∠2,再由对顶角相等,得到∠5=∠6,即可求出所求角度数;
②由三角形ADF与三角形CPF相似,得到比例式,变形得到积的恒等式,再由对顶角相等,利用两边成比例,且夹角相等的三角形相似得到三角形AFP与三角形CFD相似,利用相似三角形对应角相等得到∠APF为60°,由∠APD+∠DPC,求出∠APC为120°,进而确定出∠APB与∠BPC都为120°,即可得证.
试题解析:(1)证明:①∵∠PAB+∠PBA=180°﹣∠APB=60°,∠PBC+∠PBA=∠ABC=60°,
∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
②解:∵△ABP∽△BCP,
∴![]() ,
,
∴PB2=PAPC=12,
∴PB=2![]() ;
;
(2)解:①∵△ABE与△ACD都为等边三角形,
∴∠BAE=∠CAD=60°,AE=AB,AC=AD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△ACE和△ABD中,
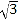 ,
,
∴△ACE≌△ABD(SAS),
∴∠1=∠2,
∵∠3=∠4,
∴∠CPD=∠6=∠5=60°;
②证明:∵△ADF∽△CFP,
∴AFPF=DFCF,
∵∠AFP=∠CFD,
∴△AFP∽△CDF.
∴∠APF=∠ACD=60°,
∴∠APC=∠CPD+∠APF=120°,
∴∠BPC=120°,
∴∠APB=360°﹣∠BPC﹣∠APC=120°,
∴P点为△ABC的费马点.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 三角形ABC各顶点在格点上
(1)直接写出三角形ABC的三个顶点的坐标
A B C ;
(2)画出三角形ABC关于y轴对称的三角形A′B′C′.
(3)求三角形ABC的面积;
(4)直接与出A′C′与y轴交点的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数图象经过点M(2,6)
(1)求这个函数的解析式,并指出它的图象位于哪些象限?
(2)在这个图象上任取两个点A(a,b)和B(a′,b′),如果a>a′,那么b和b′怎样的大小关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.

(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动3.5秒时,求出点P的坐标;
(3)在移动过程中,若点P到x轴的距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在AE的异侧,BD⊥AE于D,CE⊥AE于E.

(1)△ABD与△CAE全等吗?BD与DE+CE相等吗?请说明理由。
(2)如图2,若直线AE绕点A旋转到图②所示的位置(BD<CE)时,其余条件不变,则BD与DE、CE的关系如何?请说明理由
(3)如图3,若直线AE绕点A旋转到图③所示的位置(BD>CE)时,其余条件不变,则BD与DE、CE的关系如何?
(4)根据以上的讨论,请用简洁的语言表达BD与DE、CE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚棋子放在七角棋盘的第0号角,现依逆时针方向移动这枚棋子,其各步依次移动1,2,3,…,n个角,如第一步从0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角,….若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数y=k(x﹣ax﹣b),其中a≠b.
(1)若此二次函数图象经过点(0,k),试求a,b满足的关系式.
(2)若此二次函数和函数y=x2﹣2x的图象关于直线x=2对称,求该函数的表达式.
(3)若a+b=4,且当0≤x≤3时,有1≤y≤4,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com