
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.

(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动3.5秒时,求出点P的坐标;
(3)在移动过程中,若点P到x轴的距离为4个单位长度时,求点P移动的时间.
【答案】(1)4;6;(4,6);(2)(1,6);(3)点P移动的时间为2秒或6秒.
【解析】
(1)根据![]() +|b﹣6|=0、算术平方根的非负性及绝对值的非负性即可求出a和b,从而求出B的坐标;
+|b﹣6|=0、算术平方根的非负性及绝对值的非负性即可求出a和b,从而求出B的坐标;
(2)根据P点的速度和时间,即可求出P移动的路程,从而判断出P点所在的边,然后计算P点坐标即可;
(3)根据P到x轴的距离为4个单位长度,分类讨论即可.
解:(1)由题意得,a﹣4=0,b﹣6=0,
解得,a=4,b=6,
∴OA=4,OB=6,
∵四边形OABC为长方形,
∴点B的坐标为(4,6),
故答案为:4;6;(4,6);
(2)∵点P的速度是每秒2个单位长度,
∴点P移动3.5秒时,移动的距离为:3.5×2=7,而6<7<10
故此时P点在CB上
∴CP=7﹣6=1,且P点纵坐标为6.
∴点P的坐标(1,6);
(3)当点P在OC上时,
∵点P到x轴的距离为4个单位长度
∴此时移动的路程为4,
∴移动的时间为:4÷2=2(秒);
当点P在BA上时,
∴此时移动的路程为6+4+6﹣4=12,
∴移动的时间为:12÷2=6(秒),
综上所述,点P到x轴的距离为4个单位长度时,点P移动的时间为2秒或6秒.


科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣![]() )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.
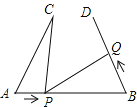
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=6![]() ,动点P从点A出发,以每秒
,动点P从点A出发,以每秒![]() 个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.
个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.

(1)当t=1秒时,求动点P、Q之间的距离;
(2)若动点P、Q之间的距离为4个单位长度,求t的值;
(3)若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com