
【题目】如图,矩形ABCD中,AB=6,BC=6![]() ,动点P从点A出发,以每秒
,动点P从点A出发,以每秒![]() 个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.
个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.

(1)当t=1秒时,求动点P、Q之间的距离;
(2)若动点P、Q之间的距离为4个单位长度,求t的值;
(3)若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度为 .
【答案】(1)7;(2),t=2或4s时,PQ=4;(3)![]() .
.
【解析】
(1)作QK⊥AD于K.根据矩形性质可知tan∠BDA=![]() ,所以∠BDA=30°,当t=1时,DQ=2,QK=
,所以∠BDA=30°,当t=1时,DQ=2,QK=![]() DQ=1,DK=
DQ=1,DK=![]() ,根据勾股定理求出PQ长即可.(2)分两种情况讨论:①当0<t≤3时,QK=t,PK=6
,根据勾股定理求出PQ长即可.(2)分两种情况讨论:①当0<t≤3时,QK=t,PK=6![]() ﹣2
﹣2![]() t,已知PQ=4,所以t2+(6
t,已知PQ=4,所以t2+(6![]() ﹣2
﹣2![]() t)2=42,求出t的值即可. ②当3<t≤6时,作QH⊥AD于H,OK⊥AD于K,OF⊥OH于F.根据根据矩形性质可知OD+OQ=AQ=2t,AH=
t)2=42,求出t的值即可. ②当3<t≤6时,作QH⊥AD于H,OK⊥AD于K,OF⊥OH于F.根据根据矩形性质可知OD+OQ=AQ=2t,AH=![]() t, 已知AP=
t, 已知AP=![]() t,所以点P与点H重合,由PQ=4即可求出t的值.(3)作OK⊥AD于K.QH⊥AD于H.由矩形性质可知OD=OA,由OK⊥AD得DK=AK,根据DH=PA=
t,所以点P与点H重合,由PQ=4即可求出t的值.(3)作OK⊥AD于K.QH⊥AD于H.由矩形性质可知OD=OA,由OK⊥AD得DK=AK,根据DH=PA=![]() t得KH=PK因为MK∥HQ,MQ=MP,所以点M在OD上时的运动距离为
t得KH=PK因为MK∥HQ,MQ=MP,所以点M在OD上时的运动距离为![]() OK=
OK=![]() .当点Q在线段OC上时,取CD的中点M′,OK的中点M,连接MM′,则点M的运动轨迹是线段MM′.根据勾股定理求出MM′的长即可,在整个运动过程中点M运动路径的长度为MM′+
.当点Q在线段OC上时,取CD的中点M′,OK的中点M,连接MM′,则点M的运动轨迹是线段MM′.根据勾股定理求出MM′的长即可,在整个运动过程中点M运动路径的长度为MM′+![]() .
.
(1)如图1中,作QK⊥AD于K.

∵四边形ABCD是矩形,
∴BC=AD=6![]() ,∠BAD=90°,
,∠BAD=90°,
∴tan∠BDA=![]() ,
,
∴∠BDA=30°,
当t=1时,DQ=2,QK=![]() DQ=1,DK=
DQ=1,DK=![]() ,
,
∵PA=![]() ,
,
∴PK=4![]() ,
,
∴PQ=![]()
![]() =7.
=7.
(2)①如图1中,当0<t≤3时,QK=t,PK=6![]() ﹣2
﹣2![]() t,
t,
∵PQ=4,
∴t2+(6![]() ﹣2
﹣2![]() t)2=42,
t)2=42,
解得t=2或![]() (舍弃)
(舍弃)
②如图2中,当3<t≤6时,作QH⊥AD于H,OK⊥AD于K,OF⊥OH于F.

由题意:AQ=2t,AH=![]() t,
t,
∵AP=![]() t,
t,
∴AH=AP,
∴P与H重合,
当PQ=4时,AQ=8,
∴2t=8,
∴t=2,
综上所述,t=2或4s时,PQ=4.
(3)如图3中,作OK⊥AD于K.QH⊥AD于H.

∵四边形ABCD是矩形,
∴OD=OA,
∵OK⊥AD,
∴DK=AK,
∵DH=PA=![]() t,
t,
∴KH=PK,
∵MK∥HQ,MQ=MP,
∴点M在线段OK上,当点Q从D到O时,点M的运动距离=![]() OK=
OK=![]() ,
,
如图4中,当点Q在线段OC上时,取CD的中点M′,OK的中点M,连接MM′,则点M的运动轨迹是线段MM′.
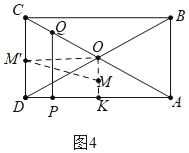
在Rt△OMM′中,MM′=![]() =
=![]() ,
,
∴在整个运动过程中;直接写出点M运动路径的长度为![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.

(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动3.5秒时,求出点P的坐标;
(3)在移动过程中,若点P到x轴的距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
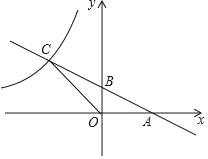
【题目】如图,直线y=-![]() x+b(b>0)与x轴、y轴分别交于点A、B,与双曲线y=-
x+b(b>0)与x轴、y轴分别交于点A、B,与双曲线y=-![]() (x<0)交于点C.
(x<0)交于点C.
(1)若△AOB的面积为2,求b的值;
(2)连接OC,若△AOC的面积为2,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚棋子放在七角棋盘的第0号角,现依逆时针方向移动这枚棋子,其各步依次移动1,2,3,…,n个角,如第一步从0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角,….若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 一同学利用直尺和圆规完成如下操作:
一同学利用直尺和圆规完成如下操作:
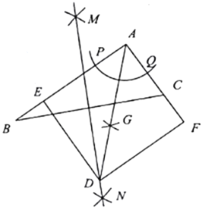
①以点![]() 为圆心,以适当的长为半径画弧,交
为圆心,以适当的长为半径画弧,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,
②分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,![]() 两点,直线
两点,直线![]() 交
交![]() 于
于![]() .
.
请你观察图形,根据操作结果解答下列问题:
(1)![]() 的度数为______;
的度数为______;
(2)作![]() 于
于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE平分∠BCD,交AB边于点E,EF∥BC,交CD于点F,点G是BC边的中点,连接GF,且∠1=∠2,CE与GF交于点M,过点M作MH⊥CD于点H.
(1)求证:四边形BCFE是菱形;
(2)若CH=1,求BC的长;
(3)求证:EM=FG+MH.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com