【题目】如图，在正方形
中，点
的坐标是
，则
点的坐标是( )
A.
B.
C.
D.
【答案】A
【解析】
作CD⊥x轴于D，作AE⊥x轴于E，由AAS证明△AOE≌△OCD，得出AE=OD，OE=CD，由点A的坐标是（-3，1），得出OE=3，AE=1，∴OD=1，CD=3，得出C（1，3）即可．
解：如图所示：作CD⊥x轴于D，作AE⊥x轴于E，
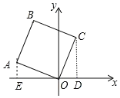
则∠AEO=∠ODC =90°，
∴∠OAE+∠AOE=90°，
∵四边形OABC是正方形，
∴OA=CO，∠AOC=90°，
∴∠AOE+∠COD=90°，
∴∠OAE=∠COD，
在△AOE和△OCD中，
，
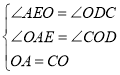∴△AOE≌△OCD（AAS），
∴AE=OD，OE=CD，
∵点A的坐标是（-3，1），
∴OE=3，AE=1，
∴OD=1，CD=3，
∴C（1，3），故选：A．
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案科目：初中数学 来源： 题型：
【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： 
．
（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果二次函数的二次项系数为1，那么此二次函数可表示为y＝x2＋px＋q，我们称[p，q]为此函数的特征数，如函数y＝x2＋2x＋3的特征数是[2，3]．
(1)若一个函数的特征数为[－2，1]，求此函数图象的顶点坐标；
(2)探究下列问题：
①若一个函数的特征数为[4，－1]，将此函数的图象先向右平移1个单位长度，再向上平移1个单位长度，求得到的图象对应的函数的特征数；
②若一个函数的特征数为[2，3]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[3，4]?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝(m－1)x2＋m2－2m－2的图象开口向下，且经过点(0，1)．
(1)求m的值；
(2)求此抛物线的顶点坐标及对称轴；
(3)当x为何值时，y随x的增大而增大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市居民用电的电价实行阶梯收费，收费标准如下表：
一户居民每月用电量x（单位：度） | 电费价格（单位：元/度） |
0＜x≤200 | a |
200＜x≤400 | b |
x＞400 | 0.92 |
（1）已知李叔家四月份用电286度，缴纳电费178.76元；五月份用电316度，缴纳电费198.56元，请你根据以上数据，求出表格中a，b的值．
（2）六月份是用电高峰期，李叔计划六月份电费支出不超过300元，那么李叔家六月份最多可用电多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.
（1）求证：△BDE≌△BCE；
（2）试判断四边形ABED的形状，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
