
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

【答案】证明见解析.
【解析】试题分析:(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵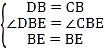 ,
,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
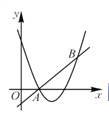
(2)求不等式x2+bx+c>x+m的解集(直接写出答案);
(3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
调查结果统计表

调查结果频数分布直方图 调查结果扇形统计图
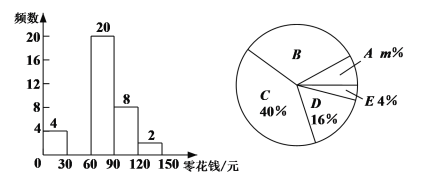
请根据以上图表,解答下列问题:
(1)填空:这次调查的样本容量是 ,![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(4)该校共有![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
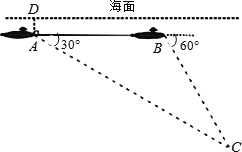
A. 2000米 B. 4000米 C. 2000米 D. (2000![]() +500)米
+500)米
查看答案和解析>>
科目:初中数学 来源: 题型:
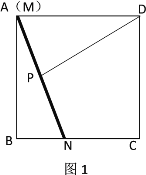
【题目】如图,有一根固定长度的木棍![]() 在正方形
在正方形![]() 的内部如图1放置,此时木棍的端点
的内部如图1放置,此时木棍的端点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 在
在![]() 边上,
边上,![]() ,将木棍沿
,将木棍沿![]() 向下滑动
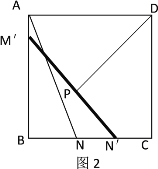
向下滑动![]() 个单位长度至图2的位置.同时另一个端点
个单位长度至图2的位置.同时另一个端点![]() 沿
沿![]() 向右滑动
向右滑动![]() 个单位长度至
个单位长度至![]() ,且
,且![]() ,
,![]() .在滑动的过程中,点
.在滑动的过程中,点![]() 到木棍中点
到木棍中点![]() 的最短距离为__________.
的最短距离为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,且
各边的中点,且![]() ,
,![]() ,
,![]() .
.

(1)试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)如图2,依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,再依次取
,再依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ……以此类推,取
……以此类推,取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,根据信息填空:
,根据信息填空:
①四边形![]() 的面积是__________;
的面积是__________;
②若四边形![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
③试用![]() 表示四边形
表示四边形![]() 的面积___________.
的面积___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,分别作∠BAD与∠ABC的平分线分别交BC于点E,交AD于点F 连接EF.

(1)补全图形;
(2)判断四边形ABEF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com