
【题目】如图1,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,且
各边的中点,且![]() ,
,![]() ,
,![]() .
.

(1)试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)如图2,依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,再依次取
,再依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ……以此类推,取
……以此类推,取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,根据信息填空:
,根据信息填空:
①四边形![]() 的面积是__________;
的面积是__________;
②若四边形![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
③试用![]() 表示四边形
表示四边形![]() 的面积___________.
的面积___________.
【答案】(1)矩形,见解析;(2)①15,②5,③![]()
【解析】
(1)根据中位线定理,得出四边形![]() 是平行四边形,再根据
是平行四边形,再根据![]() 可判断四边形
可判断四边形![]() 为矩形;
为矩形;
(2)①根据题意算出A1B1=3,A1D1=5,可得四边形![]() 的面积;
的面积;
②根据题意算出A2D2= B2C2= C2D2=B2A2=![]() ,可得四边形
,可得四边形![]() 为菱形,得出四边形
为菱形,得出四边形![]() 的面积,以此类推得出
的面积,以此类推得出![]() =
=![]() ,令
,令![]() =
=![]() ,解出n即可;
,解出n即可;
③由②可得结果;
解:(1)四边形![]() 是矩形,
是矩形,
证明:∵![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,
各边的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
同理可得![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
易得![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(2)①由题意可知:A1B1=![]() AC=3,A1D1=
AC=3,A1D1=![]() BD=5,
BD=5,
四边形![]() 的面积=3×5=15;
的面积=3×5=15;
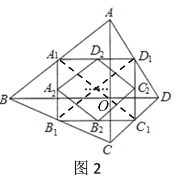
②由构图过程可得:A2D2=B2C2=![]() B1D1=
B1D1=![]()
![]() =
=![]() ,C2D2=B2A2=
,C2D2=B2A2=![]() A1C1=
A1C1=![]()
![]() =
=![]() ,
,
可知四边形![]() 为菱形,
为菱形,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
同理可求:![]() =
=![]() ,
,![]() =
=![]() ,…,
,…,![]() =
=![]() ,
,
故当四边形![]() 的面积为
的面积为![]() 时,
时,![]() =
=![]() ,
,
解得:n=5;
③由②可知:用![]() 表示四边形
表示四边形![]() 的面积为
的面积为![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.

小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P位置时,距离村庄M最近;行驶到点Q位置时,距离村庄N最近.请在图中的公路AB上分别画出点P,Q的位置(保留画图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M却越来越远?(分别用文字表述你的结论,不必证明).
(3)到在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中的AB上画出这一点(保留画图痕迹,不必证明);如果不存在,请简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
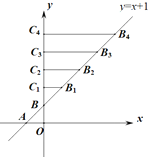
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作y 轴的垂线,垂足为点C1,得到⊿BB1C1;在直线 AB上截取B1B2= BB1,过点B2分别作y 轴的垂线,垂足为点C2,得到⊿BB2C2;在直线AB上截取B2B3= B1B2,过点B3作y 轴的垂线,垂足为点C3,得到⊿BB3C3;……;第3个⊿BB3C3的面积是___________;第n个⊿BBnCn的面积是______________(用含n的式子表示,n是正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=![]() (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com