
【题目】如图,正方形![]() 的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且
的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且![]() ,则四边形
,则四边形![]() 的面积为__________.
的面积为__________.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a-2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
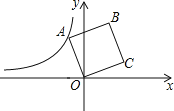
【题目】如图,在平面直角坐标系中,正方形OBCD的顶点O在坐标原点,点B的坐标为(2,5),点A在第二象限,反比例函数 的图象经过点A,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
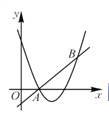
【题目】如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集(直接写出答案);
(3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,且
各边的中点,且![]() ,
,![]() ,
,![]() .
.

(1)试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)如图2,依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,再依次取
,再依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ……以此类推,取
……以此类推,取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,根据信息填空:
,根据信息填空:
①四边形![]() 的面积是__________;
的面积是__________;
②若四边形![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
③试用![]() 表示四边形
表示四边形![]() 的面积___________.
的面积___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com