
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。

【答案】(1)证明见解析(2)24
【解析】试题分析:(1)根据等腰三角形的性质,可得AC=BC,∠ACB=90°,根据余角的性质,可得∠OAC=∠BCE,根据AAS可证;
(2)根据全等三角形的性质,可得B点的坐标,根据待定系数法,可求得b的值,最后根据三角形的面积公式求解即可.
试题解析:(1)证明:∵△ABC是等腰直角三角形
∴∠ACB=900,AC=BC
∴∠ACO+∠BCE=900
BE⊥CE,∴∠BCE+∠CBE=900
∴∠ACO=∠CBE
∴△AOC≌△CEB
(2)解:∵△AOC≌△CEB
∴BE=OC=2,CE=OA=4
∴点B的坐标为(6,2)
又一次函数y=x+b经过点B(6,2)
∴2=6+b
∴b=-4
∴点D的坐标为(0,-4)
∴![]()
在△ABD中,AD边上高的长度就是B点纵坐标的绝对值.
∴S△ABD=![]() ×8×6=24
×8×6=24
∴△ABD的面积为24.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起,

(1)若∠DCE=25°,∠ACB=;若∠ACB=150°,则∠DCE=;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
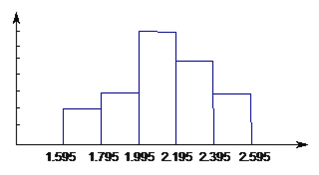
【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是![]() ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月30日,国务院关税税则委员会决定从当天起对纺织品出口关税作出进一步调整,对一些纺织品取消征收出口关税.在此背景下,某报报道了2008年1~4月份某市服装对外出口的情况,并绘制统计图如下:
请你根据统计图中提供的信息,回答下列问题:
(1)2008年1~4月份,该市服装企业出口额较多的是哪两个国家?
(2)2008年1~4月份,该市服装企业平均每月出口总额是多少万美元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com