
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在AE的异侧,BD⊥AE于D,CE⊥AE于E.

(1)△ABD与△CAE全等吗?BD与DE+CE相等吗?请说明理由。
(2)如图2,若直线AE绕点A旋转到图②所示的位置(BD<CE)时,其余条件不变,则BD与DE、CE的关系如何?请说明理由
(3)如图3,若直线AE绕点A旋转到图③所示的位置(BD>CE)时,其余条件不变,则BD与DE、CE的关系如何?
(4)根据以上的讨论,请用简洁的语言表达BD与DE、CE的数量关系.
【答案】(1)见解析;(2)BD=DE-CE,理由见解析; (3)BD=DE-CE;理由见解析;(4) 当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.
【解析】
(1)在直角三角形中,由题中条件可得∠ABD=EAC,又有AB=AC,则有一个角及斜边相等,则可判定Rt△BAD≌Rt△AEC,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;
(2)由题中条件同样可得出Rt△BAD≌Rt△AEC,得出对应线段相等,进而可得线段之间的关系;
(3)同(2)的方法即可得出结论.
(4)利用(1)(2)(3)即可得出结论.
(1)证明:在△ABD和△CAE中,
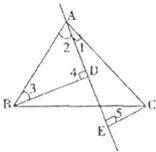
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
又∠4=∠5=90°,AB=AC,
∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.
又AE=AD+DE,
∴AE=DE+CE,
即BD=DE+CE.
(2)BD=DE-CE.
证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
又AB=AC,∠ADB=∠CEA=90°,
∴△ADB≌△CEA.
∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,
即BD=DE-CE.
(3)同(2)的方法可证:BD=DE-CE.
(4)当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.


科目:初中数学 来源: 题型:
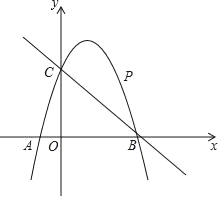
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2﹣EA2=AC2.

(1)求证:∠A=90°;
(2)若AB=8,BC=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个分数(分子、分母均为正整数)的分母比它的分子大5.
(1)若将这个分数的分子加上14,分母减去1,则所得的分数是原分数的倒数,求这个分数;
(2)若将这个分数的分子、分母同时加上4,试比较所得的分数和原分数的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(![]() ﹣1)EF.其中正确结论的个数为( )
﹣1)EF.其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com