【题目】汽车油箱中的余油量Q（升）是它行驶的时间t（小时）的一次函数，某天该汽车外出时，油箱中余油量与行驶时间的变化关系如图．
（1）根据图象，求油箱中的余油Q与行驶时间t的函数关系式；
（2）从外出开始算起，如果汽车每小时行驶50千米．当油箱中余油30升时，该汽车行驶了多少千米？
【答案】（1）Q＝﹣5t+60（0≤t≤12）；（2）300千米
【解析】
（1）根据函数图象可以设出函数的解析式，从而可以求出油箱中的余油Q与行驶时间t的函数关系式，并写出自变量t的取值范围；
（2）将Q=30代入（1）中的函数解析式，从而可以求得t的值，进而求得该汽车行驶的路程.
（1）设油箱中的余油Q与行驶时间t的函数关系式是：Q=kt+b，
，
解得：
，
∴Q=﹣5t+60，
当Q=0时，﹣5t+60=0，解得：t=12，
即油箱中的余油Q与行驶时间t的函数关系式是：Q=﹣5t+60(0≤t≤12)；
（2）当Q=30时，30=﹣5t+60，
解得：t=6，
50×6=300(千米).
即油箱中余油 30升时，该汽车行驶了300千米.
科目：初中数学 来源： 题型：
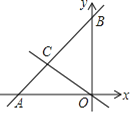
【题目】如图，一次函数
的图像与
轴
轴分别交于点
、点
，函数，与
的图像交于第二象限的点
，且点横坐标为
.
（1）求
的值；
（2）当
时，直接写出的取值范围；
（3）在直线上有一动点
，过点作轴的平行线交直线于点
，当
时，求点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有这样一个问题：探究函数y＝x+|x﹣2|的图象与性质
小明根据学习函数的经验，对函数y＝x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程，请补充完成：
（1）化简函数解析式，当x≥2时，y＝ ；当x＜2时，y＝ ；
（2）根据（1）中的结果，请在图1的坐标系中画出函数y＝x+|x﹣2|的图象；
（3）结合函数的图象，写出该函数的一条性质： ；
（4）结合画出的函数图象，利用图2解决问题，若关于x的方程ax+1＝x+|x﹣2|有两个实数根，直接写出实数a的取值范围： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑500米，先到终点的人原地休息．已知甲先出发2秒，在跑步过程中，甲．乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①100秒时乙到达终点；②a＝8；③b＝92④c＝125，其中正确的是（ ）
A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】八年级的小明同学通到这样一道数学题目：△ABC为边长为4的等边三角形，E是边AB边上任意一动点，点D在CB的延长线上，且满足AE＝BD．
（1）如图①，当点E为AB的中点时，DE＝ ；
（2）如图②，点E在运动过程中，DE与EC满足什么数量关系？请说明理由；
（3）如图③，F是AC的中点，连接EF．在AB边上是否存在点E，使得DE+EF值最小？若存在，求出这个最小值；若不存在，请说明理由．（直角三角形中，30°所对的边是斜边的一半）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．
（1）求此抛物线的解析式；
（2）求点C和点D的坐标；
（3）若点P在第一象限内的抛物线上，且S△ABP=4S△COE，求P点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题，“今有圆材，埋于壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？” 用现代的数学语言表达是：“如图，CD是⊙O的直径，弦AB⊥CD，垂足为E，CE = 1寸，AB = 1尺，求直径的长”. 依题意，CD长为（ ）
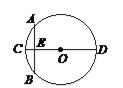
A. 
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目：初中数学 来源： 题型：
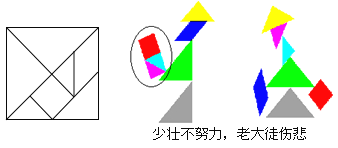
【题目】小明和小儿是同班同学，被分到了同一个学习小组，在一次数学活动课上，他们各自用一张面积为
的正方形纸片制作了一副七巧板，合作完成了如图所示的作品.请计算图中打圈部分的面积是（ ）
少壮不努力，老大徒伤悲
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
