
【题目】如图所示,在![]() 中,
中,![]() 是边
是边![]() 中点,连接
中点,连接![]() ,将
,将![]() 沿线段
沿线段![]() 翻折后得
翻折后得![]() ,其中
,其中![]() ,则
,则![]() 到
到![]() 边的距离为( )
边的距离为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
首先连接AA′,延长BD与AA′交于点E,作DF⊥AB,由翻折的性质得出△ABA′为等腰三角形,△A′CD是等边三角形,然后利用等腰三角形三线合一的性质得出BE⊥AA′,AE=A′E,进而利用勾股定理得出DE、BD,再次利用勾股定理构建方程,即可得出AF,进而得出DF.
连接AA′,延长BD与AA′交于点E,作DF⊥AB于F,如图所示:

由已知,得AB=A′B=![]() ,AD=A′D=4
,AD=A′D=4
∴△ABA′为等腰三角形,
∴BE⊥AA′,AE=A′E
∵A′C=4
∴△A′CD是等边三角形
∴∠ADA′=120°,∠EDA′=60°,∠AA′C=90°
∴DE=2,AE=A′E=![]()
∴![]()
∴BD=BE-DE=5-2=3
设AF=![]() ,在△ABD中,
,在△ABD中,![]()
∴![]()
即![]()
解得![]()
∴
故答案为D.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为(-2,1)。
(1)请直接写出A1的坐标 ;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b﹣6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,演绎推理的过程称为证明,证明的出发点和依据是基本事实.证明三角形全等的基本事实有:两边及其夹角分别相等的两个三角形全等,两角及其夹边分别相等的两个三角形全等,三边分别相等的两个三角形全等.
(1)请选择利用以上基本事实和三角形内角和定理,结合下列图形,证明:两角分别相等且其中一组等角的对边相等的两个三角形全等.

(2)把三角形的三条边和三个角统称为三角形的六个元素.如果两个三角形有四对对应元素相等,这两个三角形一定全等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 外有一点
外有一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.


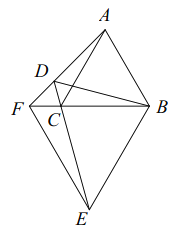
图1 图2 图3
(1)如图1,若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(2)如图2,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,以
,以![]() 为边向下作等边
为边向下作等边![]() ,若点
,若点![]() ,
,![]() ,
,![]() 在同一直线上,且
在同一直线上,且![]() ,直接写出
,直接写出![]() 的度数为___________(结果用含
的度数为___________(结果用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,巴蜀中学七年级一班同学都积极参加了植树活动.去年4月份该班同学的植树情况的部分统计如下图所示:

(1)根据以上统计图中的信息,
①该班有_____人;②植树株数的中位数是__________株;
③该班植树为5株的人数占该班总人数的百分比________________.
(2)请将该条形统计图补充完整;
(3)据统计,全年级每班植树情况大致相同,请根据该班的植树情况,估计全年级2000人中植树大于4棵的一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图.

(1)根据图象,求油箱中的余油Q与行驶时间t的函数关系式;
(2)从外出开始算起,如果汽车每小时行驶50千米.当油箱中余油30升时,该汽车行驶了多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com